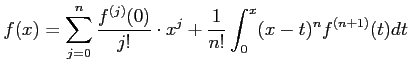Next: About this document ...
ïŋ―ïŋ―ïŋ―Ïģïŋ― IAïŋ―é―Ž No.7
ïŋ―ïŋ―ïŋ―ïŋ― 7.5
- ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ØĪÎīïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―
ïŋ―ōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ïŋ―
ïŋ―ōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
- ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ō·ŦĪïŋ―ïŋ―ÖĪïŋ―ïŋ―ïŋ―ïŋ―ČĪËĪïŋ―ęĄĒ
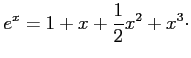
(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ÔĪÃĪïŋ―ïŋ―ïŋ―)
ïŋ―ηïŋ―ïŋ―Ξïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 7.7 (ïŋ―ïŋ―1)
ïŋ―ïŋ―ïŋ―ïŋ―2ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ŲĪïŋ―ÔĪïŋ―ÉŽïŋ―ŨĪïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆĄïŋ―ïŋ―ŅĪïĪ·ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ĘŽïŋ―ïŋ―ĘŽïŋ―ōĪĶĪÞĪïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ëĪģïŋ―ČĪËĪïŋ―ęĄĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ĮĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ëŧïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ōĪąĪëĪŋïŋ―áĄĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―
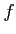
ïŋ―ïŋ―
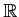
ïŋ―ïŋ―ïŋ―ÎĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ėĪŋïŋ―ïŋ―ïŋ―Ņŋïŋ―ïŋ―Âŋïŋ―ïŋ―ÍĪïŋ―
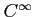
ïŋ―ïŋ―Øŋïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―Čēïŋ―ïŋ―ęĪđïŋ―ëĄĢ
(ÃĒïŋ―ïŋ―ïŋ―ŲĨïŋ―ïŋ―ČĨïŋ―ïŋ―ÍĪĮĪïŋ―ïŋ―ÃĪÆĪâĄĒ ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ï°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―)
- ïŋ―ïŋ―ĘŽïŋ―ïŋ―ĘŽïŋ―ØĪÎīïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ― 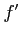 ïŋ―ËĪïŋ―ÅŽïŋ―ŅĪïŋ―ïŋ―ïŋ―(
ïŋ―ËĪïŋ―ÅŽïŋ―ŅĪïŋ―ïŋ―ïŋ―(
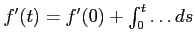 ïŋ―ηïŋ―ïŋ―Ξïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―åĄĒ)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ηïŋ―ïŋ―Ξïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―åĄĒ)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
- ïŋ―ïŋ―ĘŽïŋ―ïŋ―ĘŽïŋ―ōĪĶĪÞĪïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ëĪģïŋ―ČĪËĪïŋ―ęĄĒ
ïŋ―ōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
- ïŋ―âĪĶïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ÍĪÎĪïŋ―ïŋ―ČĪō·ŦĪïŋ―ïŋ―ÖĪïŋ―ïŋ―ïŋ―ïŋ―ČĪËĪïŋ―ęĄĒ
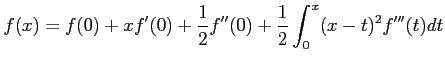 |
(T2) |
ïŋ―ōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĖĪïŋ― 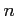 ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―
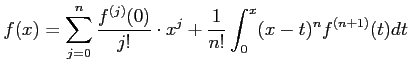 |
(Tn) |
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 7.8 (ïŋ―ïŋ―1)
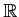
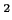
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ėĪŋ
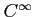
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ņŋïŋ―ïŋ―Øŋïŋ―
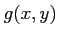
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
- (T2)ïŋ―ïŋ―ÅŽïŋ―ŅĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―)ïŋ―ņĪēïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
- ïŋ―ïŋ―ïŋ―ĖĪïŋ―
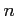 ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―(Tn)ïŋ―ïŋ―ÅŽïŋ―ŅĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―)ïŋ―ņĪēïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÏĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―)
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―(Tn)ïŋ―ïŋ―ÅŽïŋ―ŅĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―)ïŋ―ņĪēïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÏĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ― 7.9
ïŋ―ŲĨïŋ―ïŋ―ČĨïŋ―ïŋ―ÍīØŋïŋ―
ïŋ―ïŋ―
- (T2)(ïŋ―ÎĨŲĨïŋ―ïŋ―ČĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―ÅŽïŋ―ŅĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪēïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
- (Tn)(ïŋ―ÎĨŲĨïŋ―ïŋ―ČĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―ÅŽïŋ―ŅĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪēïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÏĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 7.10 (ïŋ―ïŋ―1)
ïŋ―ïŋ―ïŋ―Ņŋïŋ―ïŋ―ŲĨïŋ―ïŋ―ČĨïŋ―ïŋ―ÍīØŋïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
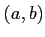
ïŋ―ïŋ―ïŋ―ïŋ―ęĪ·ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
-
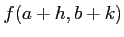 ïŋ―ïŋ―
ïŋ―ïŋ― 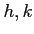 ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―1ïŋ―ïŋ―ïŋ―Îđïŋ―ÞĪĮķïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―1ïŋ―ïŋ―ïŋ―Îđïŋ―ÞĪĮķïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ŲĨïŋ―ïŋ―ČĨïŋ―
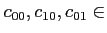
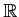
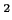 ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
-
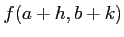 ïŋ―ïŋ―
ïŋ―ïŋ― 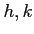 ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―2ïŋ―ïŋ―ïŋ―Îđïŋ―ÞĪĮķïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―2ïŋ―ïŋ―ïŋ―Îđïŋ―ÞĪĮķïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ŲĨïŋ―ïŋ―ČĨïŋ―
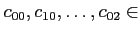
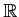
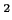 ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Íūïŋ―ïŋ―ïŋ―(ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―ĘŽïŋ―ηïŋ―ïŋ―Į―ÐĪïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 7.11 (ïŋ―ïŋ―1)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(1),(2)ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―Æ·ïŋ―ïŋ―ïŋ―ïŋ―ÖĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―äĪĩïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―æĪĻïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆļïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ĘĪïŋ―ïŋ―ïŋ―)
ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―Öūïŋ―Íūïŋ―ïŋ―ŨĪïŋ―ïŋ―ïŋ―ĘŽïŋ―Į―ÐĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 7.12 (ïŋ―ïŋ―1)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(1),(2)ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ņŋïŋ―ïŋ―Øŋïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―Æ·ïŋ―ïŋ―ïŋ―ïŋ―ÖĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―



Next: About this document ...
2009-06-30
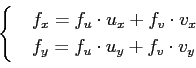
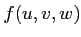 (
(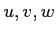 ïŋ―ïŋ―2ïŋ―Ņŋïŋ―
ïŋ―ïŋ―2ïŋ―Ņŋïŋ― 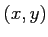 ïŋ―ÎīØŋïŋ―)
ïŋ―ÎīØŋïŋ―)
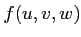 (
(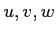 ïŋ―ïŋ―3ïŋ―Ņŋïŋ―
ïŋ―ïŋ―3ïŋ―Ņŋïŋ― 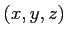 ïŋ―ÎīØŋïŋ―)
ïŋ―ÎīØŋïŋ―)
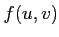 (
(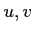 ïŋ―ïŋ―3ïŋ―Ņŋïŋ―
ïŋ―ïŋ―3ïŋ―Ņŋïŋ― 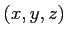 ïŋ―ÎīØŋïŋ―)
ïŋ―ÎīØŋïŋ―)
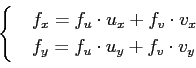
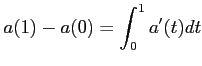
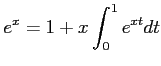
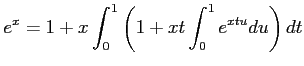
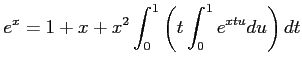
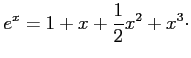 (ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ÔĪÃĪïŋ―ïŋ―ïŋ―)
(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ÔĪÃĪïŋ―ïŋ―ïŋ―)
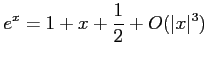
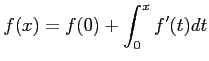
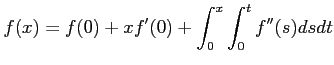
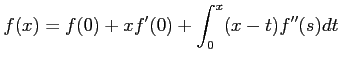
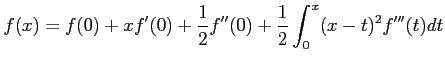
![]() ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―