


Next: About this document ...
魹ス魹ス魹スマウ魹ス IA魹ス鮨ャ No.5
魹ス魹ス魹ス魹ス 5.1
魹スヒ、ト、魹ス魹スニ。魹ス
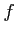
魹ス魹ス
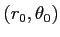
魹スヒ、魹ス魹ス魹ス魹ス魹ス魹ス魹スハャ
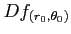
魹ス魹ス
魹ス魹ス魹スホケ魹ス魹ス魹ス
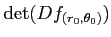
魹ス魹ス魹ス魹ス陦」
魹ス魹ス魹ス魹ス 5.2
魹スヒ、ト、魹ス魹スニ。魹ス
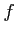
魹ス魹ス
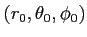
魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スハャ
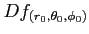
魹ス魹ス
魹ス魹ス魹スホケ魹ス魹ス魹ス
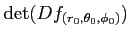
魹ス魹ス魹ス魹ス陦」
魹ス魹ス魹ス魹ス 5.3 (魹ス魹ス1)
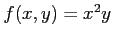
魹スヒ、魹ス魹ス魹ス魹ス魹ス魹スニ。魹ス
-
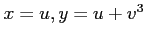 魹スネ、魹ス魹ス魹ス魹スニ。魹ス
魹スネ、魹ス魹ス魹ス魹スニ。魹ス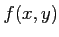 魹ス魹ス
魹ス魹ス 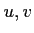 魹スヌス魹スノス魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス
魹スヌス魹スノス魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス 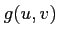 魹スネ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス
魹スネ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス
- 魹ス魹スニウ魹スリソ魹ス
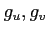 魹ス庹ス、琦セ魹ス魹ス魹ス魹ス陦」
魹ス庹ス、琦セ魹ス魹ス魹ス魹ス陦」
- 魹ス魹スハャ魹ス魹スマ「魹ス魹スホァ
魹ス庹ウ、ホセ魹ス魹スヒウホ、魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 5.4 (魹ス魹ス1)
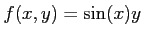
魹スヒ、魹ス魹ス魹ス魹ス魹ス魹スニ。魹ス魹ス魹ス魹ス魹ス
5.3 魹ス魹ス(2) 魹ス魹ス (3) 魹ス徸ォ、魹ス魹スヨ、魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹スムソ魹ス 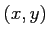 魹スホエリソ魹ス
魹スホエリソ魹ス 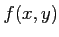 魹スヒエリ、魹ス魹ス魹ス魹ス魹ス魹ス魹スハャ魹ス魹ス魹ス魹ス魹ス魹ス
魹スヒエリ、魹ス魹ス魹ス魹ス魹ス魹ス魹スハャ魹ス魹ス魹ス魹ス魹ス魹ス
魹スマ。魹ス魹ス魹ス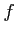 魹ス魹ス
魹ス魹ス 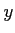 魹ス魹ス゚、魹ス魹ス
魹ス魹ス゚、魹ス魹ス 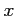 魹ス魹スニー魹ス魹ス魹ス魹ス魹ス魹ス魹スネ、魹ス魹ス魹ス魹ス魹ス魹ス魹スヌ、魹ス魹ス魹ス魹ス
魹スネ、魹ス魹ス魹ス魹ス魹ス魹スネ、魹ス魹スフ」魹ス魹ス魹スニ、魹ス魹ス槶ォ魹ス鬘「魹ス魹ス魹スホー魹ス魹スフイ魹スマ。魹ス
魹ス魹スニー魹ス魹ス魹ス魹ス魹ス魹ス魹スネ、魹ス魹ス魹ス魹ス魹ス魹ス魹スヌ、魹ス魹ス魹ス魹ス
魹スネ、魹ス魹ス魹ス魹ス魹ス魹スネ、魹ス魹スフ」魹ス魹ス魹スニ、魹ス魹ス槶ォ魹ス鬘「魹ス魹ス魹スホー魹ス魹スフイ魹スマ。魹ス
(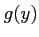 魹スマ。魹スヌ、魹スユ、ホ。ラー魹ス魹スムソ魹ス魹スリソ魹ス)
魹スネ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヘソ魹ス魹ス魹ス魹ス魹ス槩」魹スハイ魹ス魹ス魹ス魹ス魹ス魹ス魹スマ、魹ス魹ス魹ス魹スニァ魹ズ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス槶ウ魹スネ。魹ス
魹スマ。魹スヌ、魹スユ、ホ。ラー魹ス魹スムソ魹ス魹スリソ魹ス)
魹スネ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヘソ魹ス魹ス魹ス魹ス魹ス槩」魹スハイ魹ス魹ス魹ス魹ス魹ス魹ス魹スマ、魹ス魹ス魹ス魹スニァ魹ズ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス槶ウ魹スネ。魹ス
魹ス魹ス魹ス魹ス 5.5 (魹ス魹ス1)
魹ス魹ス魹スムソ魹ス
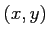
魹スホエリソ魹ス
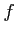
魹スヒエリ、魹ス魹ス魹ス魹ス魹ス魹ス魹スハャ魹ス魹ス魹ス魹ス魹ス魹ス
魹ス魹ス庹ュ、魹ス魹ス魹ス魹ス魹ス
-
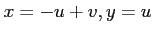 魹ス魹ス魹スムソ魹ス魹スムエ魹ス魹ス魹ス魹スニ。魹ス魹ス蠏ュ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹スムソ魹ス魹スムエ魹ス魹ス魹ス魹スニ。魹ス魹ス蠏ュ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス
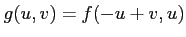 魹ス魹ス
魹スリ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヒス魹ストセ魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス
魹スリ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヒス魹ストセ魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
- 魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スハャ魹ス魹ス魹ス魹ス魹ス魹ス魹スホー魹ス魹スフイ魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 5.6
魹ス魹ス魹スムソ魹ス
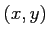
魹スホエリソ魹ス
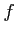
魹スヒエリ、魹ス魹ス魹ス魹ス魹ス魹ス魹スハャ魹ス魹ス魹ス魹ス魹ス魹ス
魹ス魹ス庹ュ、ハ、魹ス魹ス魹ス魹ス魹ス(魹スメ・魹ス魹ス:
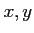
魹ス魹スナャ魹ス魹ス魹スヒー璦。魹スムエ魹ス魹ス魹ス魹スニ、゚、陦」)
魹ス魹ス魹ス魹ス 5.7
魹ス魹ス魹スムソ魹ス
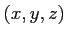
魹スホエリソ魹ス
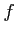
魹スヒエリ、魹ス魹ス魹ス魹ス魹ス魹ス魹スハャ魹ス魹ス魹ス魹ス魹ス魹ス
魹ス魹ス庹ュ、ハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 5.8 (魹スロ、テ、魹ス魹ス魹ス魹ス魹スマエヨー魹ステ、ニ、魹ス魹ス魹ス魹スホ、ヌ。魹ス魹ス魹ス魹ス魹ス)



Next: About this document ...
2009-05-28
![]() 魹スホエリソ魹ス
魹スホエリソ魹ス ![]() 魹スヒエリ、魹ス魹ス魹ス魹ス魹ス魹ス魹スハャ魹ス魹ス魹ス魹ス魹ス魹ス
魹スヒエリ、魹ス魹ス魹ス魹ス魹ス魹ス魹スハャ魹ス魹ス魹ス魹ス魹ス魹ス