Next: About this document ...
魹ス魹ス魹スマウ魹ス IA魹ス鮨ャ No.3
魹ス魹ス魹ス魹ス 3.2
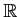
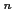
魹スホウ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス
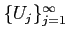
魹スヌ。魹ス魹ス魹ス魹スホカ魹ス魹ス魹ス魹ス魹スハャ
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヌ、マ、ハ、魹ス魹ス魹ス魹ス晫イ、ハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 3.3 (魹ス魹ス1.魹ス魹スヒイ庹ッ、魹ス魹スネ。魹ス)
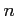
魹ス魹ス魹ス魹ス魹スホ・ル・魹ス魹スネ・魹ス
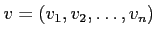
魹ス魹ス
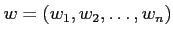
魹スネ、魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スム、魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス槩」
魹ス魹ス魹スホ、ネ、魹ス魹ス魹ス
-
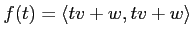 魹ス魹ス
魹ス魹ス 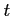 魹ス魹ス
魹ス杌。シ魹ス魹スヌ、魹ス魹ス槶ウ魹スネ、忒ィ、魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス(魹ス魹ス魹スホキ魹ス魹ス魹ス魹ス魹ス
魹ス魹ス
魹ス杌。シ魹ス魹スヌ、魹ス魹ス槶ウ魹スネ、忒ィ、魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス(魹ス魹ス魹スホキ魹ス魹ス魹ス魹ス魹ス
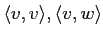 魹ス魹ス魹ス魹ス魹スム、魹ス魹スニス㖨ュ、ハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹スム、魹ス魹スニス㖨ュ、ハ、魹ス魹ス魹ス魹ス魹ス
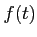 魹スホコヌセ魹ス魹スヘ、魹ス 0
魹スハセ魹スヌ、魹ス魹ス槶ウ魹スネ、ネ。魹ス魹ス杌。シ魹ス魹スホコ魹ス魹ス遑「
魹スヌセ魹ス魹ス魹ス魹スホシ魹ス魹ス魹ス魹スム、魹ス魹スニ。魹ス
魹スホコヌセ魹ス魹スヘ、魹ス 0
魹スハセ魹スヌ、魹ス魹ス槶ウ魹スネ、ネ。魹ス魹ス杌。シ魹ス魹スホコ魹ス魹ス遑「
魹スヌセ魹ス魹ス魹ス魹スホシ魹ス魹ス魹ス魹スム、魹ス魹スニ。魹ス
魹ス忒ィ、魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
-
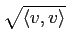 魹スホ、魹ス魹スネ、魹ス
魹スホ、魹ス魹スネ、魹ス 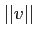 魹スネス㖨ッ、魹ス魹スネ、ヒ、魹ス魹ス魹スネ。魹ス
魹スネス㖨ッ、魹ス魹スネ、ヒ、魹ス魹ス魹スネ。魹ス
魹ス魹ス魹ス魹ス魹ス魹スホゥ魹スト、魹ス魹スネ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スネ、テ、ニシ魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス(魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス)
魹ス魹ス魹ス魹スホーハイ魹ス魹ス魹ス魹ス魹ス魹ス魹スマ。魹スマ「ツウ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス 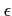 -
-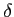 魹ス魹スヒ。魹ス魹ス魹スム、魹ス魹スニケヤ、魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹スム、魹ス魹スニイ魹ス魹ス魹ス魹ス魹ス魹ス槶ウ魹スネ。魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス
魹ス魹スヒ。魹ス魹ス魹スム、魹ス魹スニケヤ、魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹スム、魹ス魹スニイ魹ス魹ス魹ス魹ス魹ス魹ス槶ウ魹スネ。魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス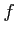 魹ス魹ス
魹ス魹ス 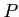 魹ス魹ス
マ「ツウ魹スヌ、魹ス魹ス魹スネ、マ。魹ス
魹ス魹ス
マ「ツウ魹スヌ、魹ス魹ス魹スネ、マ。魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス槶ウ魹スネ、ヒ、魹ス魹ス槩」テア魹スヒ。魹スマ「ツウ魹スラ、ネ、魹ス魹ス魹ス魹スミ。魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スホウ魹ス魹ス魹ス魹ス魹スマ「ツウ魹スラ、ホー魹スフ」魹スヌ、魹ス魹ス槩」
魹ス魹ス魹ス魹ス 3.4
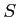
魹ス魹ス
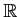
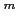
魹ス魹ス魹ス魹スハャ魹ス魹ス魹ス遑「
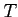
魹ス魹ス
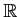
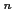
魹ス魹ス魹ス魹スハャ魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹スネ、魹ス魹ス槩」
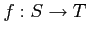
魹ス魹スマ「ツウ魹スヌ。魹ス
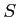
魹ス魹ス魹ス魹ス魹ス魹ス
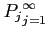
魹ス魹ス
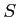
魹ス魹ス魹ス魹ス
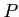
魹ス魹ス
魹ス魹スツォ魹ス魹ス魹ス魹スハ、魹スミ。魹ス魹ス魹ス魹ス魹ス
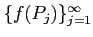
魹ス魹ス
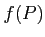
魹スヒシ魹スツォ魹ス魹ス魹ス槶ウ魹スネ、魹ス
魹ス魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 3.5
魹スホ・魹ス魹スリソ魹ス
魹ス魹スマ「ツウ魹スヌ、魹ス魹ス槶ウ魹スネ、忒ィ、魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 3.7
魹ス魹スマ「ツウ魹スヌ、魹ス魹ス槶ウ魹スネ、忒ィ、魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 3.8
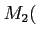
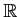
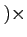
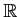
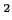
魹ス魹ス魹ス魹スハャ魹ス魹ス魹ス魹ス魹ス魹ス魹スツ、ル、魹ス
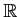
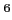
魹ス魹ス
ニア魹ス魹ス槶ケ魹ス槩」
魹ス魹ス魹スホ、ネ、魹ス魹ス魹ス
魹ス魹ス魹ス魹スネ・ル・魹ス魹スネ・魹スホ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ズ、魹ス魹ス魹ス魹ス
魹ス魹スマ「ツウ魹スヌ、魹ス魹ス槶ウ魹スネ、忒ィ、魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 3.9
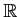
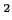
魹ス魹スホエリソ魹ス
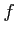
魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス槩」魹ス魹ス魹ス魹ス
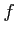
魹スマク魹ス魹ス魹ス
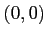
魹ス魹スマ「ツウ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 3.10
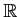
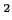
魹ス魹スホエリソ魹ス
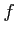
魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス槩」魹ス魹ス魹ス魹ス
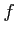
魹スマク魹ス魹ス魹ス
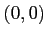
魹ス魹スマ「ツウ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス



Next: About this document ...
2009-04-21
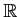
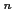 魹スホウ魹ス魹ス魹ス魹ス魹ス
魹スホウ魹ス魹ス魹ス魹ス魹ス 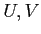 魹スホカ魹ス魹ス魹ス魹ス魹スハャ
魹スホカ魹ス魹ス魹ス魹ス魹スハャ 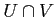 魹スマウ魹ス魹ス魹ス魹ス魹スヌ、魹ス魹ス槶ウ魹スネ、忒ィ、魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹スマウ魹ス魹ス魹ス魹ス魹スヌ、魹ス魹ス槶ウ魹スネ、忒ィ、魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
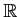
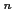 魹スホウ魹ス魹ス魹ス魹ス魹ス
魹スホウ魹ス魹ス魹ス魹ス魹ス 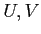 魹ス魹ス魹スツス魹ス魹ス魹ス
魹ス魹ス魹スツス魹ス魹ス魹ス 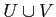 魹スマウ魹ス魹ス魹ス魹ス魹スヌ、魹ス魹ス槶ウ魹スネ、忒ィ、魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹スマウ魹ス魹ス魹ス魹ス魹スヌ、魹ス魹ス槶ウ魹スネ、忒ィ、魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
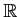
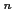 魹ス魹スフオ魹スツクト、ホウ魹ス魹ス魹ス魹ス魹ス
魹ス魹スフオ魹スツクト、ホウ魹ス魹ス魹ス魹ス魹ス
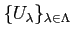 魹ス魹ス魹スツス魹ス魹ス魹ス
魹ス魹ス魹スツス魹ス魹ス魹ス