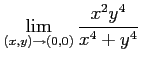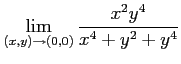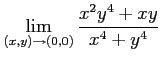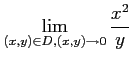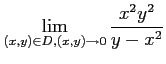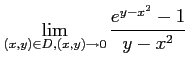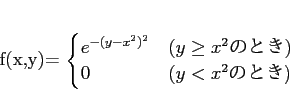Next: About this document ...
魹ス魹ス魹スマウ魹ス IA魹ス鮨ャ No.2
魹ス魹ス魹ス魹ス 2.3
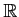
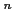
魹スホエ魹ス魹スワ・ル・魹ス魹スネ・魹ス
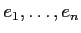
(魹ス魹ス
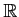
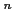
魹ス魹ス魹ス魹ス魹スネ、゚、ハ、魹ス魹ス魹ス魹ス魹ス魹ス)
魹スホ、魹ス魹ス魹ス魹スノ、魹スヌ、篏ー魹ストーロ、ハ、魹ス魹ス魹ス
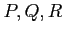
魹ス魹スネ、魹スミ。魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スムキ魹ス魹ス魹ストコ魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス魹スネ。魹ス
魹スト、゙、魹ス
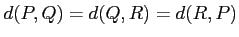
魹ス魹ス魹スハ、熙ソ魹スト、魹ス魹スネ、魹ス
魹ス魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 2.4 (魹ス魹ス魹ス魹ス魹ス魹ス1. 魹ス魹ス魹ス魹ス魹ス魹ス魹スノ、魹ス魹ス鬢ォ魹ス魹ス庹ュサマ、魹スニ、魹ス魹スノ、魹ス魹ス魹ス)
魹スツソ魹ス魹ス魹ス
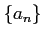
魹ス魹スヘソ魹ス魹ス魹ス魹ス魹スニ、魹ス魹ス魹スネ、魹ス魹ス槩」魹ス魹ス魹スホ、ネ、魹ス魹ス魹ス
- 魹ス魹ス魹ス魹スホカヒク魹ス
魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
- 魹スヒク魹ス
魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 2.6
魹ス魹ス魹ス魹ス
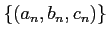
魹ス魹ス魹ス魹スツォ魹ス魹ス魹ス魹スネ、魹ス魹ス魹ス
魹ス魹ス魹ス魹ス
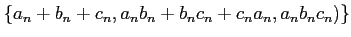
魹ス魹ス
ノャ魹ス魹ス魹ス魹スツォ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 2.7
魹ス魹ス魹ス魹スホオユ、魹ス魹ス荀ヲ魹ス魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス
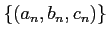
魹ス魹スヘソ魹ス魹ス魹ス魹ス魹スニ、魹ス魹スニ。魹ス
魹ス魹ス魹ス魹ス
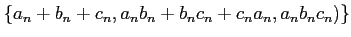
魹ス魹ス魹ス魹スツォ魹ス魹ス魹ス魹スネ、魹ス魹ス魹ス
魹ス魹スネ、魹ス魹ス魹ス魹ス魹ス
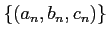
魹ス魹スノャ魹ス魹ス魹ス魹スツォ魹ス魹ス魹ス魹スネク魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 2.8
魹ス魹ス魹ス魹ス
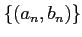
魹ス魹スヘソ魹ス魹ス魹ス魹ス魹スニ、魹ス魹スニ。魹ス
魹ス魹ス魹ス魹ス
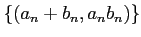
魹ス魹ス魹ス魹ス
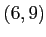
魹スヒシ魹スツォ魹ス魹ス魹ス魹スネ、魹ス魹ス魹ス
魹ス魹スネ、魹ス魹ス魹ス魹ス魹ス
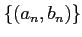
魹ス魹スノャ魹ス魹ス魹ス魹スツォ魹ス魹ス魹ス魹スネク魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 2.9 (魹ス魹ス1)
魹ス魹ス魹スホカヒクツ、魹スツク魹ス゚、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スネ、魹ス魹ス魹ス魹ス鬢ス魹スホカヒクツ、魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
(魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヘウ魹ス魹スメ、ル、槶ウ魹スネ。魹ス)
魹ス魹ス魹ス魹ス 2.10 (魹ス魹ス1)
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヌ、マ。魹ス
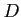
魹スマ、魹ス魹スホ、魹ス魹スホ、ホエリソ魹ス魹ス魹スハャ魹ス琦ャ 0
魹スヌ、ハ、魹ス魹ス魹ス魹ス魹ス庹オ、魹ス魹ス魹ス魹スネ、ヒ、魹ス魹ス槩」
(魹ス魹ス魹ス魹ス魹ス魹ス魹ステ、ニ。魹ス魹ス魹ス魹ス荀エ魹スネ、魹ス
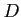
魹スマーロ、ハ、槩」)
魹ス魹スツク魹ス゚、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス
魹ス魹スツク魹ス゚、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス
魹ス魹スツク魹ス゚、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 2.11
魹スリソ魹ス
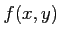
魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス槩」魹ス魹ス魹スホ、ネ、魹ス魹ス魹ス
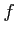
魹ス魹ス
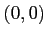
魹ス魹スマ「ツウ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス



Next: About this document ...
2009-04-15
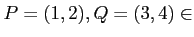
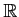
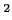 .
.
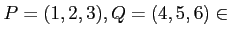
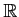
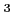 .
.
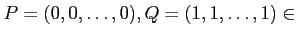
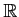
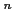 .
.