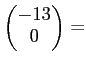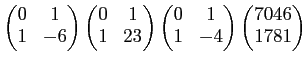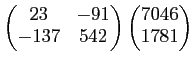๏ฟฝหคฤค๏ฟฝ๏ฟฝฦก๏ฟฝ
- ๏ฟฝ๏ฟฝ๏ฟฝฮค่คฆ๏ฟฝสค๏ฟฝฮค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝรค๏ฟฝ๏ฟฝศค๏ฟฝ๏ฟฝฦก๏ฟฝ
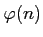 ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝสค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝสค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
- ๏ฟฝ๏ฟฝฮพ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฤฝ๏ฟฝฦฑ๏ฟฝ๏ฟฝ
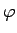 ๏ฟฝ๏ฟฝยธ๏ฟฝ฿ค๏ฟฝ๏ฟฝ๋คณ๏ฟฝศค๒ผจค๏ฟฝ๏ฟฝสค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
๏ฟฝ๏ฟฝยธ๏ฟฝ฿ค๏ฟฝ๏ฟฝ๋คณ๏ฟฝศค๒ผจค๏ฟฝ๏ฟฝสค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
-
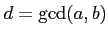 (
(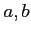 ๏ฟฝฮบ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ)๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝสค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
๏ฟฝฮบ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ)๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝสค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
-
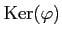 ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝสค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝสค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
-
![$ \varphi(n)=([5 d]_a, [6 d]_b) $](img8.png) ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ 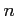 ๏ฟฝ๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝฦต๏ฟฝ๏ฟฝสค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
๏ฟฝ๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝฦต๏ฟฝ๏ฟฝสค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ