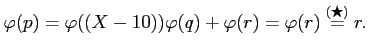�����������Ȥ��롣���ΤȤ���
-
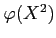 ����衣(���ΤߤǤ褤��)
����衣(���ΤߤǤ褤��)
-
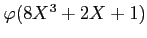 ����衣(���ΤߤǤ褤��)
����衣(���ΤߤǤ褤��)
-
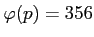 �Ȥʤ�
�Ȥʤ�
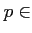
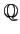
![$ [X]$](img9.png) �����
����� 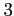 �ĵʤ�����
�����������Τ�����Ĥ� 3���ʾ�μ��Ǥ���褦�ˤ��뤳�ȡ�
(�����ȡ���ñ�ʳΤ��ỻ�ΤߤǤ褤��)
�ĵʤ�����
�����������Τ�����Ĥ� 3���ʾ�μ��Ǥ���褦�ˤ��뤳�ȡ�
(�����ȡ���ñ�ʳΤ��ỻ�ΤߤǤ褤��)
-
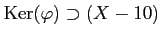
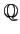
![$ [X]$](img9.png) ��������ʤ�����
��������ʤ�����
-
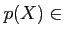
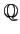
![$ [X]$](img9.png) ��
�� 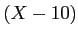 �dz�����
�dz����� 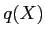 , ;���
, ;��� 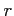 �Ȥ�����
(
�Ȥ�����
(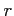 ��
�� 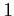 �����Ǥ�ä�;������顢 0
�������Ĥޤꡢ���(
�����Ǥ�ä�;������顢 0
�������Ĥޤꡢ���(
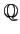 �θ�))
���ΤȤ�
�θ�))
���ΤȤ� 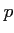 ��
�� 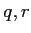 ���Ѥ���ɽ���ʤ�����(�������ס�)
���Ѥ���ɽ���ʤ�����(�������ס�)
- Ǥ�դ�
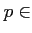
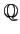
![$ [X]$](img9.png) �ˤ������ơ�
�ˤ������ơ�
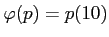 ���ʤꤿ�Ĥ��Ȥ��ʤ�����
���ʤꤿ�Ĥ��Ȥ��ʤ�����
- ��;��
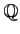
![$\displaystyle [X]/(X-10)$](img21.png)
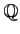
![$\displaystyle [X]
$](img22.png)
�Ǥ�¿�༰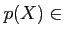
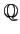
![$ [X]$](img9.png) �Υ��饹��ͭ����
�Υ��饹��ͭ���� 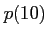 �Υ��饹������������
���ʤ�����
�Υ��饹������������
���ʤ�����
 �Ȥ������Ȥ�ֵ������������Τǡ�������ʬ�Ϻ���Ͼ���̵���˻ȤäƤ�褤��
(���֤�;͵������о�����Ȥ�äȤ褤��...)���������ɤ��ǻȤä�����
�狼��褦�����Ƥˤ��뤳�ȡ�
�Ȥ������Ȥ�ֵ������������Τǡ�������ʬ�Ϻ���Ͼ���̵���˻ȤäƤ�褤��
(���֤�;͵������о�����Ȥ�äȤ褤��...)���������ɤ��ǻȤä�����
�狼��褦�����Ƥˤ��뤳�ȡ�