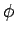 ����
����
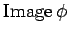 ��
�� 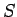 ����ʬ�ĤǤ��롣
����ʬ�ĤǤ��롣
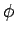 �γ�
�γ�
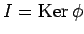 ��
�� 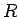 �Υ��ǥ���Ǥ��롣
�Υ��ǥ���Ǥ��롣
- ��;��
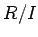 ��
��
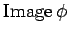 ��Ʊ���Ǥ��롣
��Ʊ���Ǥ��롣
���ιֵ�����Ⱦ�Ǥϡ����������ξ�������ɸ�Ȥ��롣
��Ⱦ�Ǥϡ��Ĥ��Τμ��㡢�Ȥ��ˡְ켡���δġ� �ˤĤ��ƾܤ���������
![]() �ԴĤ��������ʬ�Ĥ������
�ԴĤ��������ʬ�Ĥ������
�ĤȤϡ��������������ȳݤ������Ǥ��뽸��Τ��ȤǤ��롣
��ʬ�ĤȤϡ���ʬ����Ǥ��äƴĤˤʤäƤ����ΤΤ��ȤǤ��롣
�ȳݤ����ȸƤФ�����
���������Ƥ��Ƽ������������������˸�����
�������������������Ĥ���褦�ˡ� ����ƴĤ��뤳�Ȥ��Ǥ��롣 �Ĥ������Ϥ��ʤ��������δ��ĤǤ��롣 �ֿ��פ��¿�༰�פ����Ū��̾�ץ졼�䡼�Ǥ��롣 ���Ȥ��С����̤��¡��ѤˤĤ��ƤϷ��ˡ§��ʬ��ˡ§������ưŪ�� �ʤꤿ�äƤ��뤳�Ȥ�¿���� �ޤ��Ͻ�����̾������δ��Ĥ����ΤäƤ����٤��Ǥ�����:
(2) ![]() ��ñ�̸���(���ݤ���)��Ĥ��ä��Ȥ��ơ�������
��ñ�̸���(���ݤ���)��Ĥ��ä��Ȥ��ơ������� ![]() �Ȥ�����
�Ȥ�����
���ʤ����ξ�Ԥϼ¤���������
�Ĥ������ȡ�ñ�̸��ϡ������������ȸ��ä��Ȥ�������
�Ȥ��ˤϡ����������ΰ���ʬ���� �����̱���������פȤ������ͤФʤ�ʤ��Ȥ��⤢��:
�������ʤɤΡ����Τä���Τ���� ![]() ���ä��Ȥ��ơ�
���줬�Ĥˤʤ뤫���ʤ�̤�����Ƚ��ˤޤ����פʤΤϡ�
���ä��Ȥ��ơ�
���줬�Ĥˤʤ뤫���ʤ�̤�����Ƚ��ˤޤ����פʤΤϡ�
![]() �ˤ�ɬ�פʥ��С���·�äƤ��뤫���Ȥ������ȤǤ��롣
�ʤˤ������С�����·�äƤ���С�̾����Τ��Ȥ�����
���Ȥϴ��Ĥ��إܤǤ�Ǿ��¤Τ��ȤϤ��Ƥ���롣
�ˤ�ɬ�פʥ��С���·�äƤ��뤫���Ȥ������ȤǤ��롣
�ʤˤ������С�����·�äƤ���С�̾����Τ��Ȥ�����
���Ȥϴ��Ĥ��إܤǤ�Ǿ��¤Τ��ȤϤ��Ƥ���롣
����ݡ�������
�Ĥ��Τ�����������Ʋʤ����� (���¡����ιֵ��ν�λ���ޤǡ�)
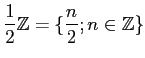
��(�̾���¡��ѤˤĤ���)�ĤǤϤʤ����Ȥ��ʤ�����