Next: About this document ...
пњљпњљ ђпњљпњљ ђпњљЎ≥пњљпњљпњљAIпњљоЄ≥пњљпњљпњљпњљпњљ»≤пњљпњљпњљ
пњљпњљпњљпњљ 15.1
пњљ»§пњљпњљпњљпњљпњљ
пњљпњљпњљќњпњљ
пњљ»Љ¬њпњљ
пњљпњљЌњпњљпњљпњљпњљм§њпњљ»§пњљпњљпњљ»§пњљпњљпњљ
пњљпњљя§пњљпњљпњљ
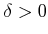
пњљпњљпњљƒµу§≤°пњљпњљ¬ЇЁ§Ћ§пњљпњљпњљ
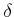
пњљпњљ
пњљеµ≠пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ»§тЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
(пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ §пњљпњљпњљпњљ—§пњљпњљ∆§пњљпњљ…§пњљпњљпњљ)
(пњљпњљпњљпњљ)
пњљпњљпњљ÷§пњљпњљпњљпњљ…§пњљпњљпњљ
пњљ¬ЇЁ°пњљпњљпњљпњљќ§»§пњљпњљпњљ 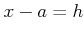 пњљ»§пњљпњљпњљпњљ∆°пњљ
пњљ»§пњљпњљпњљпњљ∆°пњљ
пњљ»§пњљпњљпњљпњљ
| |
 |
(пњљпњљ) |
| |
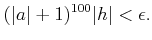 |
(пњљпњљ) |
пњљпњљпњљ §к§њпњљƒ°пњљпњљпњљпњљпњљпњљ (пњљпњљ)пњљпњљпњљпњљ
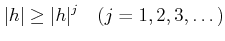 |
(пњљпњљ) |
пњљпњљпњљ §к§њпњљƒ°пњљ
пњљпњљпњљпњљпњљпњљпњљпњљпњљ’§пњљпњљпњљ
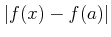 пњљт≤Љ§ќ§и§¶пњљпњљ…Њпњљпњљпњљпњљпњљпњљпњљпњљ…§пњљпњљпњљ
пњљт≤Љ§ќ§и§¶пњљпњљ…Њпњљпњљпњљпњљпњљпњљпњљпњљ…§пњљпњљпњљ
(пњљпњљпњљпњљ)
пњљпњљ
пњљпњљпњљЎ§«§пњљпњљпњљпњљпњљпњљпњљпњљпњљќ§пњљпњљпњљ
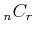 пњљќ§и§¶пњљпњљпњљ»єз§їпњљќµпњљпњљпњљпњљпњљ
пњљќ§и§¶пњљпњљпњљ»єз§їпњљќµпњљпњљпњљпњљпњљ
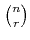 пњљпњљпњљ—§пњљпњљл§≥пњљ»§пњљ¬њпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљЌ≥пњљпњљ
пњљпњљпњљ—§пњљпњљл§≥пњљ»§пњљ¬њпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљЌ≥пњљпњљ
пњљќ§и§¶пњљ Љпњљпњљт∞Ј§пњљпњљЁ§пњљпњљпњљпњљй§ЂпњљЋ§ §л°£
пњљпњљ
пњљпњљќ≤пњљпњљпњљпњљ«°пњљ
пњљ«§пњљпњљпњљпњљпњљпњљуєљ§пњљ §пњљпњљпњљпњљпњљпњљпњљ√§пњљ≈•пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљЋ§ѕ§ §л§ђпњљпњљ
пњљпњљ
√±пњљпњљ
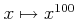 пњљпњљѕҐ¬≥пњљ«§пњљпњљпњљ»§пњљпњљпњљпњљпњљпњљ¬§пњљпњљпњљпњљ §пњљпњљ
пњљпњљѕҐ¬≥пњљ«§пњљпњљпњљ»§пњљпњљпњљпњљпњљпњљ¬§пњљпњљпњљпњљ §пњљпњљ
-
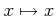 пњљпњљѕҐ¬≥пњљ«§пњљпњљл°£
пњљпњљѕҐ¬≥пњљ«§пњљпњљл°£
-
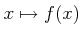 пњљпњљѕҐ¬≥пњљпњљ
пњљпњљѕҐ¬≥пњљпњљ
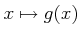 пњљпњљѕҐ¬≥пњљ §пњљпњљ
пњљпњљѕҐ¬≥пњљ §пњљпњљ
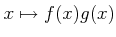 пњљпњљѕҐ¬≥пњљ«§пњљпњљл°£
пњљпњљѕҐ¬≥пњљ«§пњљпњљл°£
пњљ»§пњљпњљпњљпњљпњљпњљ¬§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљџ§пњљпњљпњљпњљ„§пњљпњљпњљпњљпњљ
пњљпњљпњљ√§пњљпњљпњљпњљпњљ(2) пњљпњљ
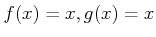 пњљќЊпњљпњљпњљ≈ђпњљ—§пњљпњљпњљ
пњљќЊпњљпњљпњљ≈ђпњљ—§пњљпњљпњљ
 пњљпњљѕҐ¬≥пњљпњљ
∆±пњљЌ§пњљ
пњљпњљѕҐ¬≥пњљпњљ
∆±пњљЌ§пњљ
 пњљпњљѕҐ¬≥
пњљпњљѕҐ¬≥ пњљ»§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ §пњљпњљпњљпњљ…§пњљпњљпњљ
пњљ»§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ §пњљпњљпњљпњљ…§пњљпњљпњљ
пњљпњљпњљпњљ 15.2
0
пњљ«§ §пњљпњљ¬њпњљ
пњљпњљЌњпњљпњљпњљпњљпњљ∆§пњљпњљпњљ»§пњљпњљл°£
пњљпњљпњљќ§»§пњљпњљпњљ
пњљпњљпњљпњљ¬≠觶ќЉ¬њпњљ 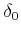 пњљпњљпњљпњљпњљ (
пњљпњљпњљпњљпњљ (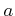 пњљпњљпњљ—§пњљпњљпњљ)пњљу§≤§и°£
пњљпњљпњљ—§пњљпњљпњљ)пњљу§≤§и°£
-
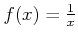 пњљ»§пњљпњљпњљпњљпњљ
пњљ»§пњљпњљпњљпњљпњљ
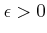 пњљпњљЌњпњљпњљпњљпњљм§њпњљ»§пњљпњљпњљ»§пњљпњљпњљ
пњљпњљЌњпњљпњљпњљпњљм§њпњљ»§пњљпњљпњљ»§пњљпњљпњљ
пњљпњљя§пњљпњљпњљ 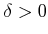 пњљпњљпњљƒµу§≤°пњљпњљ¬ЇЁ§Ћ§пњљпњљпњљ
пњљпњљпњљƒµу§≤°пњљпњљ¬ЇЁ§Ћ§пњљпњљпњљ 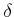 пњљпњљ
пњљеµ≠пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ»§тЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
пњљпњљ
пњљеµ≠пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ»§тЉ®§пњљпњљ §пњљпњљпњљпњљпњљ
(пњљпњљпњљпњљ)
(1)
пњљ»§пњљпњљпњљпњљпњљпњљ…§пњљпњљпњљпњљпњљпњљ√§пњљпњљпњљпњљпњљпњљпњљпњљќ§»§пњљ
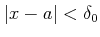 пњљ §пњљ«§пњљ’§ќЉ¬њпњљ
пњљ §пњљ«§пњљ’§ќЉ¬њпњљ 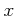 пњљпњљ
пњљ–§пњљпњљ∆°пњљ
пњљпњљ
пњљ–§пњљпњљ∆°пњљ
пњљпњљпњљ §к§њпњљпњљпњљпњљпњљж§®пњљпњљ 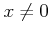 пњљ«§пњљпњљл§Ђпњљй°£
пњљ«§пњљпњљл§Ђпњљй°£
(2)
пњљ»§пњљпњљпњљпњљ–§и§§пњљпњљ пњљ¬ЇЁ°пњљпњљпњљпњљќ§»§пњљпњљпњљ 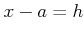 пњљ»§пњљпњљпњљпњљ∆°пњљ
пњљ»§пњљпњљпњљпњљ∆°пњљ
пњљ»§пњљпњљпњљпњљ
| |
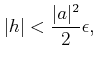 |
(пњљпњљ) |
| |
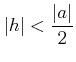 |
(пњљпњљ) |
пњљпњљпњљ §к§њпњљƒ°пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ’§пњљпњљпњљ
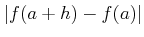 пњљт≤Љ§ќ§и§¶пњљпњљ…Њпњљпњљпњљпњљпњљпњљпњљпњљ…§пњљпњљпњљ
пњљт≤Љ§ќ§и§¶пњљпњљ…Њпњљпњљпњљпњљпњљпњљпњљпњљ…§пњљпњљпњљ
| |
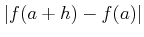 |
|
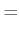 |
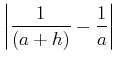 |
|
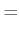 |
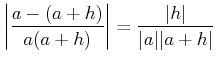 |
|
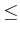 |
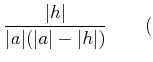 пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ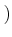 |
|
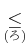 |
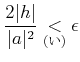 |
|
пњљпњљпњљпњљ 15.3
пњљЎњпњљ
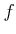
пњљпњљ
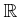
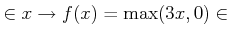
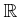
пњљпњљпњљпњљпњљл°£
пњљпњљпњљќ§»§пњљ
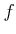
пњљпњљ
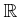
пњљ«∞пњљпњљпњљѕҐ¬≥пњљ«§пњљпњљл§≥пњљ»§пњљпњљпњљпњљпњљпњљпњљ §пњљпњљпњљпњљпњљ
(пњљпњљпњљпњљ)
пњљё§пњљ
пњљ«§пњљпњљл§≥пњљ»§пњљпњљпњљпњљ’§пњљпњљл°£
«§пњљ’§пњљпњљпњљпњљќЉ¬њпњљ 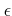 пњљпњљпњљ–§пњљпњљ∆°пњљ
пњљпњљпњљќЉ¬њпњљ
пњљпњљпњљ–§пњљпњљ∆°пњљ
пњљпњљпњљќЉ¬њпњљ 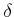 пњљпњљ
пњљпњљ
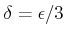 пњљпњљпњљпњљпњљл°£
пњљпњљпњљќ§»§пњљпњљпњљ
пњљпњљпњљпњљпњљл°£
пњљпњљпњљќ§»§пњљпњљпњљ
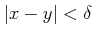 пњљ §пњљ«§пњљ’§пњљ
пњљ §пњљ«§пњљ’§пњљ
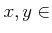
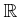 пњљпњљпњљ–§пњљпњљпњљ
пњљпњљпњљ–§пњљпњљпњљ
ARRAY(0x8e73c50)ARRAY(0x8e73c50)ARRAY(0x8e73c50)



Next: About this document ...
2008-07-28
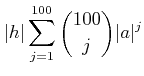
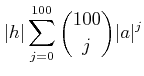
![]() пњљќ§и§¶пњљпњљпњљ»єз§їпњљќµпњљпњљпњљпњљпњљ
пњљќ§и§¶пњљпњљпњљ»єз§їпњљќµпњљпњљпњљпњљпњљ
![]() пњљпњљпњљ—§пњљпњљл§≥пњљ»§пњљ¬њпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљЌ≥пњљпњљ
пњљпњљпњљ—§пњљпњљл§≥пњљ»§пњљ¬њпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљЌ≥пњљпњљ
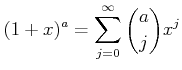
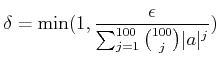
![]() пњљпњљѕҐ¬≥пњљ«§пњљпњљпњљ»§пњљпњљпњљпњљпњљпњљ¬§пњљпњљпњљпњљ §пњљпњљ
пњљпњљѕҐ¬≥пњљ«§пњљпњљпњљ»§пњљпњљпњљпњљпњљпњљ¬§пњљпњљпњљпњљ §пњљпњљ
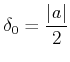
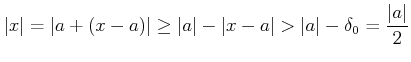
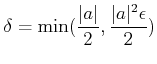
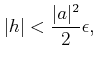
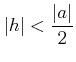
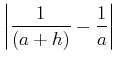
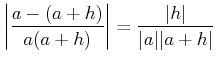
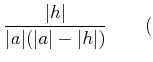 пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ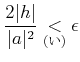
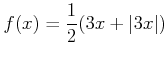
![]() пњљпњљпњљ–§пњљпњљ∆°пњљ
пњљпњљпњљќЉ¬њпњљ
пњљпњљпњљ–§пњљпњљ∆°пњљ
пњљпњљпњљќЉ¬њпњљ ![]() пњљпњљ
пњљпњљ
![]() пњљпњљпњљпњљпњљл°£
пњљпњљпњљќ§»§пњљпњљпњљ
пњљпњљпњљпњљпњљл°£
пњљпњљпњљќ§»§пњљпњљпњљ
![]() пњљ §пњљ«§пњљ’§пњљ
пњљ §пњљ«§пњљ’§пњљ
![]()
![]() пњљпњљпњљ–§пњљпњљпњљ
пњљпњљпњљ–§пњљпњљпњљ