��ߤ���
(Ʊ�����꤬�Ǥ�櫓�ǤϤ���ޤ��ºݤ�����Ϥ����� �������Ǥ��礦��)
��ߤ���
(����)
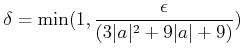
���֤����ɤ��� �ºݡ����ΤȤ���
�Ȥ����
| (��) | ||
| (��) |
| (��) |
(ȯŸ)
��� ![]() ��
��
![]() �ǰ���Ϣ³�ǤϤʤ����Ȥ��ʤ�����
�ǰ���Ϣ³�ǤϤʤ����Ȥ��ʤ�����
��ߤ���
(����)
�Ȥ����Ф褤�� �ºݡ����ΤȤ���
�Ȥ����
| (��) | ||
| (��) |
| (��) |
| (��) |
���ʤꤿ�ġ����������դ���
![]() �Τ褦��ɾ��������ɤ���
�Τ褦��ɾ��������ɤ���
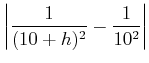 |
||
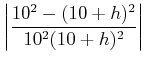 |
||
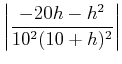 |
||
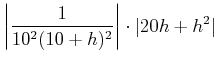 |
||
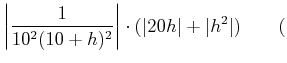 ���������� ���������� |
||
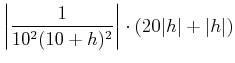 |
||
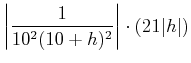 |
||
 |
![]()
ARRAY(0x8e74070)ARRAY(0x8e74070)