


Next: About this document ...
��ʬ��ʬ�س���AI���� No.12
���Τ��Ȥϡ���ñ�������ѽ��פǤ��롣
���� 12.1
- �ؿ�
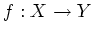 ����ñ�ͤʤ�С�
����ñ�ͤʤ�С� 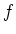 �εռ�����¸�ߤ��롣
�εռ�����¸�ߤ��롣
- �դ� �ؿ�
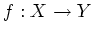 ���ռ�������Ĥʤ�С�
���ռ�������Ĥʤ�С�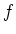 ����ñ�ͤǤ��롣
����ñ�ͤǤ��롣
- �ؿ�
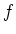 �εռ����ϡ�¸�ߤ���а��Ū�Ǥ��롣
�εռ����ϡ�¸�ߤ���а��Ū�Ǥ��롣
Ϣ³�ؿ��ξ��Ϥɤ��Ǥ������������ѿ��Ǥϴؿ���ñĴ���������ˤʤ롣
��� 12.1 (``1.3.6'')
�¿��Τ�����
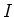
��������줿�ؿ�
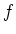
������ñĴ���ôؿ��Ǥ���Ȥϡ�
��ߤ����Ȥ��ˤ�����
���� 12.2 (``���ʽ�����1.16'')
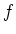
���Ķ��
![$ [a,b]$](img6.png)
��ζ���ñĴ���ä�Ϣ³�ؿ��Ǥ���С�
�εմؿ�
��¸�ߤ��롣
����ˡ�����
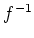
��Ϣ³�ǡ����Ķ���ñĴ���äǤ��롣
�ä������㤦��������Ϣ³���ˤĤ��Ƥ�Ҳ𤷤Ƥ�������
(�Ȥ��Τ���ش�����ʬ���ΤȤ���)
��� 12.2
�¿�ľ������ʬ����
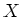
��������줿�ؿ�
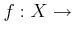
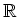
��
����Ϣ³�Ǥ����Ȥϡ�
���ʤꤿ�ĤȤ��ˤ�����
�� 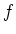 ��
�� 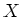 ��Ϣ³�Ǥ��뤳�Ȥ�
��Ϣ³�Ǥ��뤳�Ȥ�
��ɽ������뤳�Ȥ����դ��褦��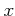 ��
�� 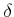 ���о������ա�
���о������ա�
�� 12.1 (����Ϣ³�ʴؿ��Ȥ����Ǥʤ��ؿ�)
��
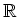 ���Ϣ³��������Ϣ³�ǤϤʤ���
���Ϣ³��������Ϣ³�ǤϤʤ���
��
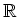 ���Ϣ³�ǡ�����Ϣ³�Ǥ⤢�롣
���Ϣ³�ǡ�����Ϣ³�Ǥ⤢�롣
�����������ֽ̾�ˡ����ε���Ǥ��롣�����϶��ʽ��
���ȤΤ��ȡ�
���� 12.3
�Ķ��
![$ [a,b]$](img6.png)
���Ϣ³�ؿ�
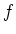
��
����Ϣ³�Ǥ��롣
���� 12.1
�ؿ��ؿ�
��
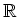
��Ǥϰ���Ϣ³�ǤϤʤ����Ȥ��ʤ�����
(â�����ؿ�ˡ§
��
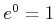
,
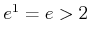
�Ͼ����ʤ����Ѥ��Ƥ��ɤ����ޤ�����Ǽˡ�ˤ���ưפ������뼰
���Ѥ����ɤ���)
2008-06-27
![]()
![]() ��
�� ![]() ��Ϣ³�Ǥ��뤳�Ȥ�
��Ϣ³�Ǥ��뤳�Ȥ�