![]()
���ʤꤿ�ĤȤ��ˤ�����
�˸¤�����ˤ�ꡢ�������ϼ��Τ褦�˸����������롣
(��)
![]()
�������ǡ� ![]() ��
�� ![]() ��
�� ![]() �ε�Υ��
�ε�Υ��
![]() ��
�� ![]() ��
��
![]() �ε�Υ�Ǥ��뤳�Ȥ����դ��롣��������ˤ��Ϣ³���Ρ�����פ�
¿�ѿ��ؿ��䡢��Υ���֤Τ������μ�����Ϣ³���������
���Τޤް��̲����뤳�Ȥ��Ǥ��롣
�ε�Υ�Ǥ��뤳�Ȥ����դ��롣��������ˤ��Ϣ³���Ρ�����פ�
¿�ѿ��ؿ��䡢��Υ���֤Τ������μ�����Ϣ³���������
���Τޤް��̲����뤳�Ȥ��Ǥ��롣
��������ϡ������פǤϤ��뤬��
Ϣ³��������ˤ����� ``![]() '' �Ρ��㳰Ū�ʰ����פ�������Ƥष��
�����ʷ��Ƥ��롣�����Ǥ��ιֵ��ǤϤ�äѤ�Ϣ³����Τ����ˤ�
���������(��)��Ƚ�ꤹ�뤳�Ȥˤ��롣
'' �Ρ��㳰Ū�ʰ����פ�������Ƥष��
�����ʷ��Ƥ��롣�����Ǥ��ιֵ��ǤϤ�äѤ�Ϣ³����Τ����ˤ�
���������(��)��Ƚ�ꤹ�뤳�Ȥˤ��롣
�����������ο�
�����������ο�
��
![]() �����ꡣ
�����ꡣ
���̤ˡ�
�������äơ�(��)�����ꡢ���ʤ���� ��![]() ��
�� ![]() ��Ϣ³�Ǥʤ��פ��Ȥϡ�
���Τ褦�˽�ɽ�����Ȥ��Ǥ��롣
��Ϣ³�Ǥʤ��פ��Ȥϡ�
���Τ褦�˽�ɽ�����Ȥ��Ǥ��롣
(��)
![]() ����
���� ![]()
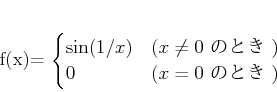
���������Ȥ���