


Next: About this document ...
ïŋ―ïŋ―ĘŽïŋ―ïŋ―ĘŽïŋ―Øģïŋ―ïŋ―ïŋ―AIïŋ―ïŋ―ïŋ―ïŋ― No.9

ïŋ―ïŋ―ïŋ―ïŋ― 9.1 (``ïŋ―ïŋ―ïŋ―Ę―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―1.9'')
3ïŋ―ÄĪïŋ―
ïŋ―Øŋïŋ―
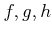
ïŋ―ïŋ―ïŋ―ïŋ― ïŋ―Âŋïŋ―
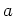
ïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―
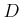
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ęĄĒ
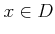
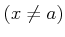
ïŋ―ĮĄïŋ―
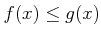
ïŋ―ČĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
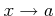 ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ― 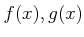 ïŋ―ÎķËļÂĪïŋ―ïŋ―ČĪïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ïŋ―ÐĄïŋ―
ïŋ―ÎķËļÂĪïŋ―ïŋ―ČĪïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ïŋ―ÐĄïŋ―
-
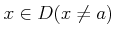 ïŋ―ïŋ―ïŋ―Ï°ÏĪĮĄïŋ―
ïŋ―ïŋ―ïŋ―Ï°ÏĪĮĄïŋ―
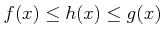 ïŋ―ĮĪïŋ―ïŋ―ÃĪÆĄïŋ―
ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ÃĪÆĄïŋ―
ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
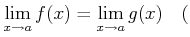
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÍĪïŋ― $A$ ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĪČĪïŋ―ïŋ―ïŋ―ČĄïŋ― 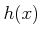 ïŋ―ïŋ―
ïŋ―ïŋ― 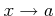 ïŋ―ÎĪČĪïŋ―ïŋ―ÎķËļÂĪïŋ―Âļïŋ―ßĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ÎĪČĪïŋ―ïŋ―ÎķËļÂĪïŋ―Âļïŋ―ßĪïŋ―ïŋ―ÆĄïŋ―
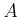 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 9.2
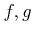
ïŋ―ïŋ―
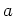
ïŋ―ÎķáĪŊïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ęĄĒ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ėĪūïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
-
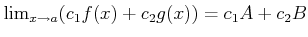 . (ÃĒïŋ―ïŋ―
. (ÃĒïŋ―ïŋ―
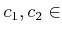
 .)
.)
-
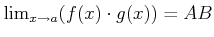 .
.
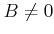 ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ΞÂŋïŋ―
ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ΞÂŋïŋ― 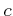 ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ÆĄïŋ― 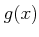 ïŋ―ïŋ―
ïŋ―ïŋ―
 ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―) 0
ïŋ―Ęģïŋ―ïŋ―ïŋ―ïŋ―ÍĪïŋ―ČĪęĄĒ
ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―) 0
ïŋ―Ęģïŋ―ïŋ―ïŋ―ïŋ―ÍĪïŋ―ČĪęĄĒ
ïŋ―ïŋ―ïŋ―ïŋ― 9.1
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ΞÂŋïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îŋïŋ―
ïŋ―ïŋ―ïŋ―ãĪĒïŋ―ïŋ―ïŋ―ÆĄïŋ―ïŋ―šÝĪïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
Ėŋïŋ―ïŋ― 9.3
ïŋ―Øŋïŋ―
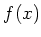
ïŋ―ïŋ―
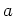
ïŋ―ÎķáĪŊïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ęĄĒ
ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĪČĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
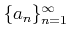
ïŋ―ïŋ―
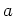
ïŋ―Ëžïŋ―ÂŦïŋ―ïŋ―ïŋ―ïŋ―ÐĄïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
Ėŋïŋ―ïŋ― 9.4
ïŋ―Øŋïŋ―
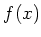
ïŋ―ïŋ―
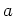
ïŋ―ïŋ―ÞĪāģŦïŋ―ïŋ―ïŋ―
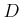
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ęĄĒïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―
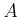
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―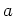 ïŋ―Ëžïŋ―ÂŦïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Ëžïŋ―ÂŦïŋ―ïŋ―ïŋ―ïŋ― 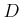 ïŋ―ïŋ―ïŋ―ĮĪïŋ―ÕĪÎŋïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĮĪïŋ―ÕĪÎŋïŋ―ïŋ―ïŋ―
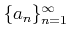 ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĄïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ÐĄïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
2008-06-18
![]()
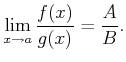
![]() ïŋ―Ëžïŋ―ÂŦïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Ëžïŋ―ÂŦïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―ïŋ―ĮĪïŋ―ÕĪÎŋïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĮĪïŋ―ÕĪÎŋïŋ―ïŋ―ïŋ―
![]() ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―