


Next: About this document ...
пњљпњљ ђпњљпњљ ђпњљЎ≥пњљпњљпњљAIпњљпњљпњљпњљ No.3
пњљпњљ¬Ђпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ 2.4пњљ«љ“§ў§пњљпњљћ§пњљ«§пњљпњљл°£
пњљпњљпњљпњљ«§пњљпњљпњљпњљ 2.4 пњљпњљ»љпњљпњљЋ°пњљпњљпњљпњљпњљпњљпњљпњљ 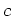 пњљпњљЌ£пњљпњљƒ§пњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљЌ£пњљпњљƒ§пњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљпњљ 3.1
пњљпњљпњљпњљ
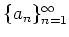
пњљпњљ(пњљпњљпњљпњљЌ§пњљпњљќ§пњљпњљб§њпњљ»§пњљпњљпњљ)
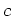
пњљЋЉпњљ¬Ђпњљпњљпњљпњљ
(пњљћ§ќњЌ§пњљпњљќ§пњљпњљб§њпњљ»§пњљпњљпњљ)
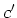
пњљЋ§пњљпњљ¬Ђпњљпњљпњљпњљ §й°Ґ
пњљ«§пњљпњљл°£пњљƒ§ё§к°ҐпњљпњљпњљпњљќЉпњљ¬Ђпњљпњљпњљ¬Єпњљя§пњљпњљпњљ»§пњљпњљпњљпњљпњљЌ£пњљпњљƒ§пњљпњљпњљпњљ §пњљпњљпњљ
пњљпњљпњљпњљпњљ«°пњљпњљƒ§пњљпњљќ§и§¶пњљпњљпњљпњљпњљпњљпњљпњљл§≥пњљ»§пњљпњљ«§пњљпњљл°£
пњљпњљпњљ 3.1
пњљпњљпњљпњљ
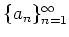
пњљпњљпњљпњљпњљпњљпњљ
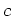
пњљЋЉпњљ¬Ђпњљпњљпњљпњљ»§пњљпњљпњљ
пњљ»љс§§§∆°пњљ
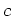
пњљќ§пњљпњљ»§пњљ
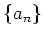
пњљпњљ
пњљЋЄпњљпњљ»Є∆§÷°пњљ
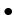 пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљпњљ 3.2 (``пњљпњљпњљпњљ1.2'')
-
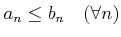 пњљ«°пњљпњљпњљпњљпњљ
пњљ«°пњљпњљпњљпњљпњљ 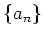 ,
, 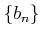 пњљпњљ
пњљпњљ¬Ђпњљпњљпњљпњљ §й°Ґ
пњљпњљ
пњљпњљ¬Ђпњљпњљпњљпњљ §й°Ґ
-
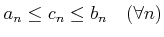 пњљ«°пњљпњљпњљпњљпњљ
пњљ«°пњљпњљпњљпњљпњљ 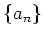 ,
, 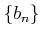 пњљпњљ
∆±пњљпњљпњљпњљ
пњљпњљ
∆±пњљпњљпњљпњљ 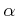 пњљЋЉпњљ¬Ђпњљпњљпњљпњљ §й°Ґ
пњљЋЉпњљ¬Ђпњљпњљпњљпњљ §й°Ґ 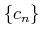 пњљпњљ
пњљпњљ 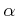 пњљЋЉпњљ¬Ђпњљпњљпњљл°£
пњљЋЉпњљ¬Ђпњљпњљпњљл°£
пњљпњљпњљпњљ 3.3 (``пњљпњљпњљпњљ1.3'')
пњљпњљ¬ЂпњљпњљпњљпњљпњљпњљпњљпњљЌ≠пњљпњљпњљ«§пњљпњљл°£
пњљпњљпњљпњљ 3.4 (``пњљпњљпњљпњљ1.4'')
пњљ¬њпњљпњљпњљ
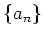
,
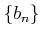
пњљѕ§пњљпњљм§Њпњљпњљпњљ¬Ђпњљпњљпњљпњљ»§пњљпњљл°£пњљпњљпњљќ§»§пњљпњљпњљ
- пњљ÷ґЋЄ¬§пњљ»§пњљ„§»§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£пњљпњљпњљ §пњљпњљпњљпњљ
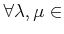
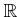 пњљпњљпњљ–§пњљпњљпњљ
пњљпњљпњљ–§пњљпњљпњљ
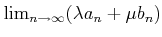 пњљѕЉпњљ¬Ђпњљпњљпњљ∆°пњљ
пњљѕЉпњљ¬Ђпњљпњљпњљ∆°пњљ
- пњљ÷Љ¬њпњљпњљќЊпњљЋ°пњљпњљѕҐ¬≥пњљ«§пњљпњљл°£пњљпњљ
- пњљ¬њпњљпњљќљпњљЋ°пњљѕ°пњљѕҐ¬≥пњљ„§«§пњљпњљл°£ пњљпњљ√§»Њ№§пњљпњљпњљпњљпњљпњљпњљпњљ»°пњљ
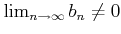 пњљ §й°Ґ
Ќ≠пњљ¬Єƒ§пњљпњљг≥∞пњљпњљпњљпњљпњљпњљпњљ
пњљ §й°Ґ
Ќ≠пњљ¬Єƒ§пњљпњљг≥∞пњљпњљпњљпњљпњљпњљпњљ 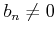 пњљ«§пњљпњљ√§∆°пњљ
пњљ«§пњљпњљ√§∆°пњљ
пњљпњљпњљ 3.2
пњљ¬њпњљпњљпњљ
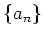
пњљпњљ√±ƒіпњљпњљпњљ√§«§пњљпњљпњљ»§ѕ°пњљ
пњљпњљпњљ §к§њпњљƒ§»§пњљпњљЋ§пњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљпњљпњљпњљпњљѕ°пњљпњљпњљпњљќ§ќњпњљпњљпњљпњљпњљћ§пњљќ§ќњпњљ (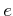 пњљ §пњљ) пњљпњљпњљпњљ–§пњљпњљ»§пњљпњљпњљЌ≠пњљпњљпњљ«§пњљпњљл°£
пњљ §пњљ) пњљпњљпњљпњљ–§пњљпњљ»§пњљпњљпњљЌ≠пњљпњљпњљ«§пњљпњљл°£
пњљпњљпњљпњљ 3.5 (``пњљпњљпњљпњљ1.5'')
пњљпњљпњљЌ≠пњљпњљпњљпњљ√±ƒіпњљпњљпњљ√њпњљпњљпњљѕЉпњљ¬Ђпњљпњљпњљл°£
пњљпњљпњљпњљ 3.1
пњљ¬њпњљпњљпњљ
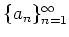
пњљпњљ
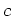
пњљЋЉпњљ¬Ђпњљпњљпњљпњљ»§пњљпњљпњљ
пњљѕЉпњљ¬Ђпњљпњљпњљпњљ»Єпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ §пњљ–§пњљпњљќЉпњљ¬ЂпњљпњљпњљпњљпњљЌ≥пњљт°ҐЄпњљпњљпњљпњљ §пњљпњљ §пњљпњљ
»њпњљпњљпњљпњљпњљ §пњљпњљпњљпњљпњљ
(пњљпњљпњљпњљ: пњљпњљпњљпњљќє÷µпњљпњљ«Њпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљт§њ§пњљпњљ—§пњљпњљпњљќ§«§ѕ§ §пњљпњљпњљ
пњљпњљ¬Ђпњљпњљпњљпњљпњљпњљпњљпњљпњљ√§пњљ (
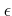
-
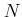
пњљпњљЋ°пњљпњљ)пњљпњљпњљпњљпњљпњљпњљл§≥пњљ»°пњљ)



Next: About this document ...
2008-04-24
![]()
![]() пњљпњљЌ£пњљпњљƒ§пњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљЌ£пњљпњљƒ§пњљпњљпњљпњљпњљпњљпњљпњљпњљ
![]() пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
![]() пњљ §пњљ) пњљпњљпњљпњљ–§пњљпњљ»§пњљпњљпњљЌ≠пњљпњљпњљ«§пњљпњљл°£
пњљ §пњљ) пњљпњљпњљпњљ–§пњљпњљ»§пњљпњљпњљЌ≠пњљпњљпњљ«§пњљпњљл°£