DEFINITION 12.1
Let
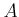
be a ring of characteristic
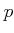
.
We equip
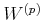
with the ring strucure defined by binary operations
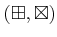
.
Then we call a ring
the ring of Witt vectors of length 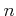
.
Its elements are called
Witt vectors of lenth 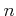
.
Note that
may be considered as a set
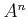
with a ring structure
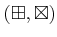
(other than the usual one).
PROOF..
Since
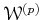
is a unital commutative ring,
there naturally exists a natural ring homomorphism
Let us first fix a positive integer
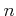
and
examine the kernel
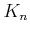
of a map
where
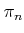
is the natural projection.
Since
we have
In other words,
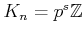
for some integer
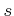
.
On the other hand, we have
thus
This implies that
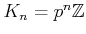
and therefore we have an inclusion
which turns to be a bijection
(
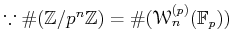
).
We then take a projective limit of the both hand sides and obtain
the resired isomorphism.
![]()