![]()
We call
![$\displaystyle \frac{1}{n}\boxdot [1]= (1-T)^{\frac{1}{n}}=
1+\sum_{j=1}^\infty \binom{\frac{1}{n}}{j} (-T)^j.
$](img17.png)
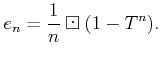
as an element of
![$\displaystyle \binom{\frac{1}{n}}{k}\in \mathbb{Z}\left[\frac{1}{n}\right].
$](img27.png)
![$\displaystyle \binom{\frac{1}{n}}{k}\in \mathbb{Z}\left[\frac{1}{n}\right]$](img29.png) | ||
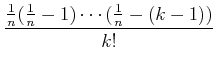 | ||
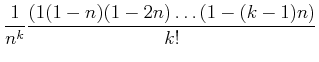 |
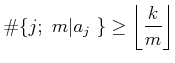
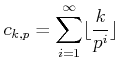
(which is evidently a finite sum in practice.) Then
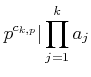
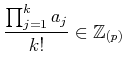
(2): Apply (1) to the cases where
![]() and count the
powers of
and count the
powers of ![]() which appear in
which appear in ![]() .
.
(3): Easy.
(4) is a direct consequence of (2),(3).
![]()
![$\displaystyle f=
\bigvee
_{\substack{
n>1\\
p\not \vert n
}}
e_n
(=[1]\boxmi...
...{^\boxtimes }
\prod_
{\substack
{p \not \vert n\\
n>1
}}
([1]\boxminus e_n))
$](img54.png)
Then ![]() defines a direct product decomposition
defines a direct product decomposition
Furthermore, the factor algebra
The following proposition tells us the importance of
the ring of ![]() -adic Witt vectors.
-adic Witt vectors.
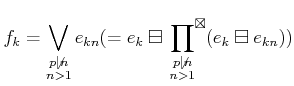
Then ![]() defines a direct product decomposition
defines a direct product decomposition
Furthermore, the factor algebra
To understand the mechanism which appears in the proposition above, it would be better to prove the following
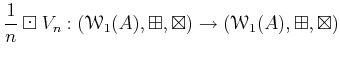
is a ring homomorphism. Its image is equal to the range of the idempotent
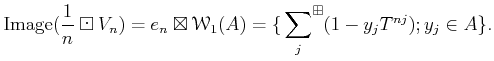
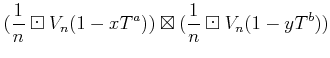 | ||
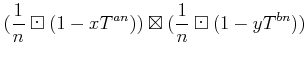 | ||
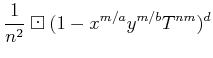 | ||
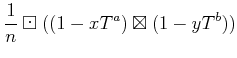 |
![]()
In preparing from No.7 to No.10 of this lecture, the following reference (especially its appendix) has been useful:
http://www.math.upenn.edu/~chai/course_notes/cartier_12_2004.pdf
ARRAY(0x8b0c098)