DEFINITION 09.1
Let
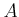
be any commutative ring.
Let
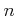
be a positive integer. Let us define additive operators
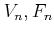
on
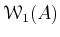
by the following formula.
(The latter definition is a formal one. That means,
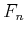
is
actually defined to be the unique continuous additive map which
satisfies
)
PROOF..
Using the rule as in the previous lemma, we see that addition descends to
an addition
of
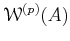
.
It is easier to see that the multiplication also descends.
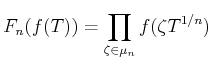
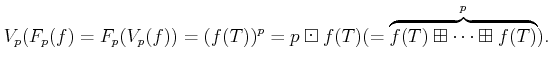
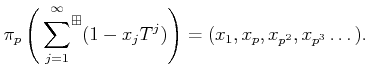
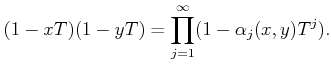
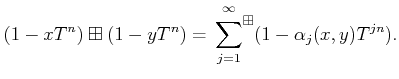
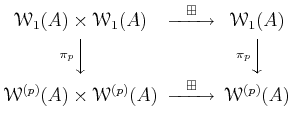
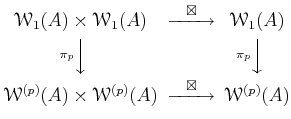
![]()