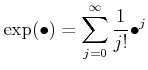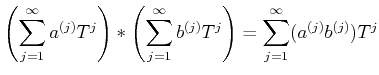Next: Bibliography
 ,
,
 , and the ring of Witt vectors
, and the ring of Witt vectors
No.07:

From here on, we make use of several notions of category theory.
Readers who are unfamiliar with the subject is advised to see
a book such as [1] for basic definitions and first properties.
Let 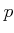 be a prime number.
For any commutative ring
be a prime number.
For any commutative ring 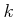 of characteristic
of characteristic 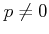 , we want to
construct a ring
, we want to
construct a ring 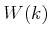 of characteristic 0
in such a way that:
of characteristic 0
in such a way that:
-
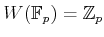 .
.
-
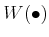 is a functor. That means,
is a functor. That means,
- For any ring homomorphism
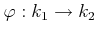 between rings of characterisic
between rings of characterisic 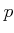 ,
there is given a unique ring homomorphism
,
there is given a unique ring homomorphism
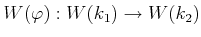 .
.
-
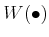 should furthermore
commutes with compositions of homomorphisms.
should furthermore
commutes with compositions of homomorphisms.
To construct 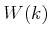 , we construct a new addition and multiplication on a
, we construct a new addition and multiplication on a
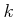 -module
-module
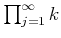 . The ring
. The ring 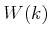 will then be called
the ring of Witt vectors.
The treatment here
essentially follows the treatment which appears in [2, VI,Ex.46-49],
with a slight modification (which may or may not be good-it may even be wrong)
by the author.
will then be called
the ring of Witt vectors.
The treatment here
essentially follows the treatment which appears in [2, VI,Ex.46-49],
with a slight modification (which may or may not be good-it may even be wrong)
by the author.
We first introduce a nice idea of Witt.
DEFINITION 07.1
Let
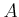
be a ring (of any characteristic).
Let
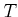
be an indeterminate.
We define the following copies of
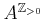
.
LEMMA 07.2
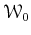 and
and
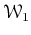 are functors from the category of
rings to the category of sets. They are represented by
``polynomial rings in infinite indeterminates''
are functors from the category of
rings to the category of sets. They are represented by
``polynomial rings in infinite indeterminates''
and
That means, there are functorial bijections
and
DEFINITION 07.3
We define the following ``universal elements''.
LEMMA 07.4
There is an well-defined map
If 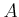 contains an copy of
contains an copy of
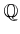 , then the map is a bijection. The inverse is
given by
, then the map is a bijection. The inverse is
given by
PROOF..
To see that
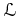
is well defined (that is, ``defined over
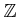
''), we compute
as follows.
The rest should be obvious.
Note: the condition
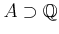 is required to guarantee exictence of
exponential
is required to guarantee exictence of
exponential
and existence of the integration
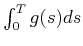 .
.
DEFINITION 07.5
We equip
![$ \mathcal W_0(A)=T A[[T]]$](img36.png)
with the usual addition and the following
(unusual) multiplication:
It is easy to see that
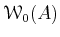
forms a (unital associative)
commutative ring with these binary operations.
DEFINITION 07.6
Let
be a ring which contains a copy of
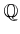
. Then we define ring structure on
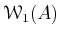
by putting
PROOF..
easy
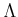
We may thus extend the definition
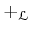 on
on
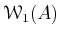 to cases
where the condition
to cases
where the condition
 is no longer satisfied.
is no longer satisfied.



Next: Bibliography
2008-07-08
![]() be a prime number.
For any commutative ring
be a prime number.
For any commutative ring ![]() of characteristic
of characteristic ![]() , we want to
construct a ring
, we want to
construct a ring ![]() of characteristic 0
in such a way that:
of characteristic 0
in such a way that:
![]() , we construct a new addition and multiplication on a
, we construct a new addition and multiplication on a
![]() -module
-module
![]() . The ring
. The ring ![]() will then be called
the ring of Witt vectors.
The treatment here
essentially follows the treatment which appears in [2, VI,Ex.46-49],
with a slight modification (which may or may not be good-it may even be wrong)
by the author.
will then be called
the ring of Witt vectors.
The treatment here
essentially follows the treatment which appears in [2, VI,Ex.46-49],
with a slight modification (which may or may not be good-it may even be wrong)
by the author.
![$\displaystyle \mathcal W_0(A)=
T A[[T]]
=
\left\{
\sum_{j=1}^\infty x^{(j)}T^j ; x^{(n)} \in A(\forall n)
\right \}
$](img16.png)
![$\displaystyle \mathcal W_1(A)=
1+ TA[[T]]
=
\left\{
1+\sum_{j=1}^\infty y_j T^j ; x_n \in A(\forall n)
\right\}
$](img17.png)
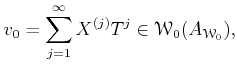
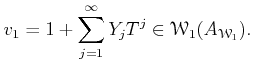
![$\displaystyle {\mathcal L}_A=-T\frac{d}{dT}\log(\bullet): 1+T A[[T]] \to T A[[T]].
$](img26.png)
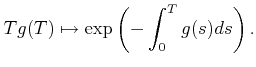
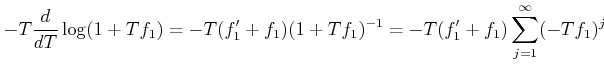
![]() is required to guarantee exictence of
exponential
is required to guarantee exictence of
exponential