


Next: About this document ...
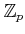 ,
,
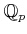 , and the ring of Witt vectors
, and the ring of Witt vectors
No.05:
In this lecture, rings are assumed to be unital, associative and
commutative unless otherwise specified.
DEFINITION 05.1
A (unital commutative) ring
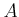
is said to be a
local ring
if it has only one maximal ideal.
PROPOSITION 05.3
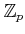 is a local ring. Its maximal ideal is equal to
is a local ring. Its maximal ideal is equal to
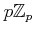 .
.
We may do some ``analysis'' such as Newton's method to obtain some
solution to algebraic equations.
Newton's method for approximating a solution of algebraic equation.
Let us solve an equation
in
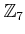 .
We first note that
.
We first note that
hold. So let us put
![$ x_0=3=[0.3]_7$](img10.png) as the first approximation of the solution.
The Newton method tells us that for an approximation
as the first approximation of the solution.
The Newton method tells us that for an approximation 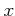 of the equation
of the equation 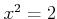 , a number
, a number 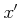 calculated as
calculated as
gives a better approximation.
So
![$ [0.3\dot{1}]_7$](img16.png) is a better approximation of the solution.
In order to make the calculation easier,
let us choose
is a better approximation of the solution.
In order to make the calculation easier,
let us choose
![$ x_1=[0.31]_7$](img17.png) (insted of
(insted of 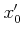 ) as a second approximation.
) as a second approximation.
We choose
![$ x_2=[0.312]_7$](img20.png) as a second approximation.
as a second approximation.
We choose
![$ x_3=[0.31261]_7$](img22.png) as a third approximation.
as a third approximation.
We choose
![$ x_4=[0.312612124]_7$](img24.png) as a third approximation.
as a third approximation.
EXERCISE 05.1
Compute
![$ [0.5]_7/[0.11]_7$](img28.png)
EXERCISE 05.2
Find a solution to
such that
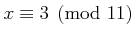
.



Next: About this document ...
2008-06-10
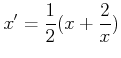
![$\displaystyle x_0'=\frac{1}{2}([0.3]_7+[0.3\dot{2}]_7=[0.3\dot{1}]_7
$](img15.png)
![% latex2html id marker 624
$\displaystyle x_1'
=\frac{1}{2}([0.31]_7+2/[0.31]_7)
=\frac{1}{2}([0.31]_7+[0.3\dot{1}45\dot{2}]_7)\fallingdotseq [0.312]_7
$](img19.png)
![]() as a second approximation.
as a second approximation.
![% latex2html id marker 628
$\displaystyle x_2'
=\frac{1}{2}([0.312]_7+2/[0.3\dot{1}2534066\dot{2}]_7)\fallingdotseq
[0.31261]_7
$](img21.png)
![]() as a third approximation.
as a third approximation.
![% latex2html id marker 632
$\displaystyle x_3'
=
=\frac{1}{2}([0.31261]_7+[0.3126142465066\dots]_7)\fallingdotseq
[0.312612124...]_7
$](img23.png)
![$\displaystyle =\frac{1}{2}([0.312612124]_7+[0.312612124565220422662213135351\dots]_7)$](img26.png)