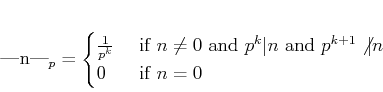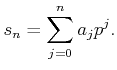Next: About this document ...
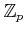 ,
,
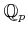 , and the ring of Witt vectors
, and the ring of Witt vectors
Yoshifumi Tsuchimoto
No.02:

Let 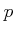 be a prime (``base'').
We would like to introduce a metric on
be a prime (``base'').
We would like to introduce a metric on
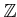 such that
such that
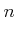
:small
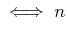
is divisible by powers of
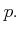
Namely:
DEFINITION 02.1
Let
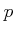
be a prime number.
- We define a
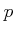 -adic norm
-adic norm
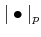 on
on
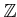 as follows.
as follows.
- We define a
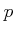 -adic distance
-adic distance
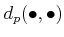 on
on
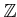 as follows.
as follows.
DEFINITION 02.3
A metric space
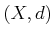
is said to be
complete
if every Cauchy sequence of
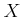
converges to an element of
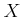
.
THEOREM 02.4
Let 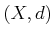 be a metric space. There exists a complete metric space
be a metric space. There exists a complete metric space
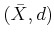 with an isometry
with an isometry
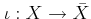 such that
such that 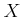 is dense
in
is dense
in 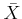 . Furthermore,
. Furthermore, 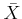 is unique up to a unique isometry.
is unique up to a unique isometry.
DEFINITION 02.5
Let
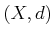
be a metric space. We call
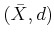
as in the above theorem
the completion of
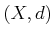
.
DEFINITION 02.6
Let
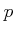
be a prime number. We denote the completion of
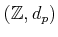
by
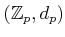
and call it
the ring of 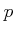 -addic integers
-addic integers.
Thus elements of
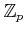
are
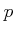 -addic integers
-addic integers.
THEOREM 02.7
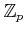 has a unique structure of a topological ring.
Namely,
has a unique structure of a topological ring.
Namely,
- There exists unique continuous maps
(addition)
and
(multiplication)
which are extensions of the usual addition and multiplication of
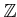 .
.
-
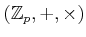 is a commutative associative ring.
is a commutative associative ring.
DEFINITION 02.8
Let
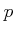
be a prime number.
For any sequence
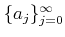
such that
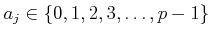
,
we consider a sequence
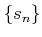
defined by
Then the sequence
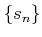
is a Cauchy sequence in
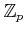
.
We denote the limit of the sequence as



Next: About this document ...
2008-06-10
![]()
![]() be a prime (``base'').
We would like to introduce a metric on
be a prime (``base'').
We would like to introduce a metric on
![]() such that
such that