


: 魹ス魹ス魹ス魹スハク魹ス魹スヒ、ト、魹ス魹ス魹ス...
魹ス魹ス魹スワク璇サヒ。 No.5
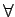 魹ス魹ス
魹ス魹ス 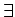 (魹ス魹ス魹ス魹ス2)
(魹ス魹ス魹ス魹ス2)
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヒ、マ。魹ス魹ス魹ス魹スニ、魹ス 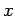 魹スヒ、ト、魹ス魹スニー魹ス魹スニ、ヒ・魹ス魹ス魹ス魹ステ・魹ス魹ス魹ス魹ス魹スノャ魹スラ、魹ス魹ス魹ス魹ス槩」
(魹ス魹ス魹ス魹ス魹ス魹ス魹ステ、ニ。魹ス魹ス魹ス魹スフ、ヒ、マイ魹ス魹ス鬢ォ魹スホケ魹スフッ魹スハ。魹スツソ魹ス魹ス魹スホ・魹スホ、庹オ、ミ、魹ス魹スラ・ニ・魹ス魹スヒ・テ・魹ス魹ス魹ス
ノャ魹スラ、ヒ、ハ、槩」) 魹スヒ、ト、魹ス魹スニー魹ス魹スニ、ヒ・魹ス魹ス魹ス魹ステ・魹ス魹ス魹ス魹ス魹スノャ魹スラ、魹ス魹ス魹ス魹ス槩」
(魹ス魹ス魹ス魹ス魹ス魹ス魹ステ、ニ。魹ス魹ス魹ス魹スフ、ヒ、マイ魹ス魹ス鬢ォ魹スホケ魹スフッ魹スハ。魹スツソ魹ス魹ス魹スホ・魹スホ、庹オ、ミ、魹ス魹スラ・ニ・魹ス魹スヒ・テ・魹ス魹ス魹ス
ノャ魹スラ、ヒ、ハ、槩」)
|
魹ス魹ス:
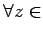
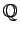
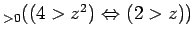 魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス
魹スハ、魹ス魹スハ、鬘「ヌ、魹スユ、魹ス魹ス魹ス魹ス魹スヘュ魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス
魹スハ、魹ス魹スハ、鬘「ヌ、魹スユ、魹ス魹ス魹ス魹ス魹スヘュ魹ス魹ス魹ス魹ス 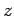 魹ス魹ス魹スミ、魹ス魹スニ。魹ス
魹ス魹ス魹ス魹ス魹ス魹スヌ、魹ス魹ス槩」
魹ス魹ス魹スミ、魹ス魹スニ。魹ス
魹ス魹ス魹ス魹ス魹ス魹スヌ、魹ス魹ス槩」
|
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヒ、マ。魹ス魹ス魹スト、魹ス魹スノ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス庹「、魹ス魹ス魹ス魹ス魹スノ、魹ス魹ス魹ス
魹ス魹ス魹スホ、ネ、魹ス魹スマ。魹ス魹スヌ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スナェ魹ス魹ス魹ス网ャ魹ス隍、魹ス魹ス
|
魹ス魹ス:
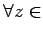
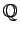
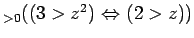 魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス
魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス
魹スヌ、魹ス魹ス槩」魹スハ、魹ス魹スハ、鬘「魹ス魹ス魹ス魹スヘュ魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス
魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス
魹スヌ、魹ス魹ス槩」魹スハ、魹ス魹スハ、鬘「魹ス魹ス魹ス魹スヘュ魹ス魹ス魹ス魹ス 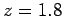 魹ス魹スヘ、魹ス魹ス魹スネ。魹ス
魹ス魹スヘ、魹ス魹ス魹スネ。魹ス
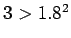 魹スヌ、マ、ハ、魹ス(
魹スヌ、マ、ハ、魹ス(
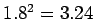 )魹スホ、魹ス
)魹スホ、魹ス 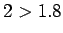 魹ス魹ス魹ス魹ス魹ス魹スヌ、魹ス魹ス槩」
魹ス魹ス魹ス魹ス魹ス魹スヌ、魹ス魹ス槩」
魹ス魹ス魹スフ、ヒ。魹ス
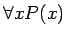 魹ス魹ス魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス
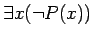 魹スヌ、魹ス魹ス遙「
魹スヌ、魹ス魹ス遙「
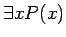 魹ス魹ス魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス
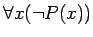 魹スヌ、魹ス魹ス槩」
魹ス魹ス魹ス魹ス魹ス魹ス魹ステ、ニ。魹ス魹ス网ィ魹ス魹ス
魹スヌ、魹ス魹ス槩」
魹ス魹ス魹ス魹ス魹ス魹ス魹ステ、ニ。魹ス魹ス网ィ魹ス魹ス
魹スネ、魹ス魹ス魹ス魹ス魹ス魹スヒ。魹ス
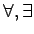 魹ス魹ズ、魹ス魹スフソ魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヒエ魹ステア魹ス魹ス魹ストキ魹ス魹ス魹スナェ魹ス魹ス魹ス魹ス魹ス槶ウ魹スネ、魹ス魹スヌ、魹ス魹ス槩」
魹ス魹ズ、魹ス魹スフソ魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヒエ魹ステア魹ス魹ス魹ストキ魹ス魹ス魹スナェ魹ス魹ス魹ス魹ス魹ス槶ウ魹スネ、魹ス魹スヌ、魹ス魹ス槩」
魹ス魹ス魹ス魹ス魹ス魹スハ」魹ス魹ス魹スヒ、ハ、テ、ニ、魹ス魹ス魹ス魹ス隍ヲ魹スヒエ魹ス魹ス魹ス魹ス魹ス琦ソ魹ス鬘「 魹ス魹ス魹ステ、魹ス魹ス朁ュケ魹ス魹ス
魹ス魹スト・魹ス魹ス㖨、、ニ、゚、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スネ、顬ォ魹ス魹ス荀ケ魹ス魹ス魹スハ、槶ウ魹スネ、魹スツソ魹ス魹ス魹ス魹ス
魹ズ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スホ、隍ヲ魹スヒ。魹ス魹ス魹ス魹スト、魹ス魹スヒカ魹ス魹スレ、テ、ニケヘ、魹ス魹ス魹スホ、魹ス魹スヒ。魹スヌ、魹ス魹ス槩」
魹ス魹ス魹ス魹ス魹ス魹ス魹スヒー魹ス魹ス魹ス魹ス魹スユ、庹キ、ニ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス
フソ魹ス魹ス 5.1
魹ス魹ス魹スフ、ヒ。魹ス魹ス魹ス魹スホシツソ魹ス
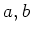
魹ス魹ス魹スミ、魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹スホゥ魹スト、ホ、魹ス
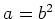
魹スホ、ネ、魹ス魹スヌ。魹ス魹ス魹ス魹ス魹ス魹ス筅ス魹スホ、ネ、魹ス魹スヒクツ、槩」
ハソ魹ス魹ス19ヌッ11魹ス魹ス29魹ス魹ス
![]() 魹ス魹ス魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス
![]() 魹スヌ、魹ス魹ス遙「
魹スヌ、魹ス魹ス遙「
![]() 魹ス魹ス魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス
![]() 魹スヌ、魹ス魹ス槩」
魹ス魹ス魹ス魹ス魹ス魹ス魹ステ、ニ。魹ス魹ス网ィ魹ス魹ス
魹スヌ、魹ス魹ス槩」
魹ス魹ス魹ス魹ス魹ス魹ス魹ステ、ニ。魹ス魹ス网ィ魹ス魹ス