


Next: About this document ...
documentclass[12pt]amsart
usepackageeucal,amssymb
par
newedtheoremtheorem����[section]newedtheoremnitheorem���ޤ���פǤʤ�����[section]renewedcommandthenitheorem
newedtheoremrefpropPropositionrenewedcommandtherefprop
newedtheoremcor��[section]newedtheoremlemma����[section]newedtheoremfact����[section]newedtheoremproposition[theorem]̿��newedtheoremaxAxiompar
theoremstyledefinition
newedtheoremdfn���[section] newedtheoremexmp��[section] newedtheoremexample��[section]newedtheoremdefinition���[section] newedtheoremq����[section] newedtheoremexq����[section] newedtheoremkeywd���ؤΥ������par
theoremstyleremark
newedtheoremrem����[section]newedtheoremclaim[]renewedcommandtheclaim par
numberwithinequationsection
par
newedcommandtheoremref[1]Theorem ref#1
newedcommandsecref[1]Sref#1
newedcommandlemref[1]Lemma ref#1
par
newedcommandZmbox
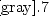 newedcommandQmbox
newedcommandQmbox
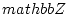 newedcommandRmbox
newedcommandRmbox
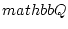 newedcommandNmbox
newedcommandNmbox
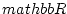 newedcommandImbox
newedcommandImbox
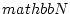 par
newedcommandLeg[2]mbox
par
newedcommandLeg[2]mbox
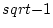 newedcommandFpmbox
newedcommandFpmbox
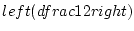 newedcommandkpekembox
newedcommandkpekembox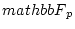 newedcommandbigzerolsmashhboxhuge 0
newedcommandbigzerousmashlower1.7exhboxhuge 0
par
setlengthtopmargin-1.5cm
setlengthtextheight26cm
begindocument
renewedcommandthepage
title[����� I No.thistime ]����� I No.thistime �����
quad
vskip-3pc
maketitle
par
setcountersectionthistime
par
noindent
par
newedcommandmymondaiI
�Ľ�Ʊ��
newedcommandbigzerolsmashhboxhuge 0
newedcommandbigzerousmashlower1.7exhboxhuge 0
par
setlengthtopmargin-1.5cm
setlengthtextheight26cm
begindocument
renewedcommandthepage
title[����� I No.thistime ]����� I No.thistime �����
quad
vskip-3pc
maketitle
par
setcountersectionthistime
par
noindent
par
newedcommandmymondaiI
�Ľ�Ʊ��
�ǡ�
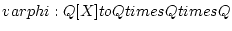 ����������ΤˤĤ���
�ͤ������� ���Τ褦�ʤ�Τ����ä��Ȥ��ơ�
beginenumerate
item
����������ΤˤĤ���
�ͤ������� ���Τ褦�ʤ�Τ����ä��Ȥ��ơ�
beginenumerate
item
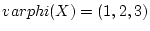 �Ϥ�����ˤʤ�٤�����������
item
�Ϥ�����ˤʤ�٤�����������
item
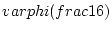 �Ϥ�����ˤʤ�٤�����������
item
�Ϥ�����ˤʤ�٤�����������
item
![$ p(X)in Q [X]$](img13.png) �ˤ������ơ�
�ˤ������ơ� 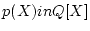 ����ʤ�����
endenumerate
par
par
newedcommandmymondaiII
begintheorem_type[q][q][section][definition][][]
����ʤ�����
endenumerate
par
par
newedcommandmymondaiII
begintheorem_type[q][q][section][definition][][]
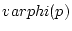 ����
���� 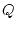 �ؤδĽ�Ʊ����¸�ߤ������������endtheorem_type
par
newedcommandmymondaiIII
begintheorem_type[q][q][section][definition][][]
�Ľ�Ʊ��
�ؤδĽ�Ʊ����¸�ߤ������������endtheorem_type
par
newedcommandmymondaiIII
begintheorem_type[q][q][section][definition][][]
�Ľ�Ʊ��
��ͤ��롣 (��������![$ [n]_{m}$](img18.png) �� ����
�� ���� 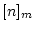 ��
�� 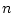 �ˤ�����
���饹��魯��)
par
beginenumerate
item
�ˤ�����
���饹��魯��)
par
beginenumerate
item 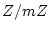 ����衣
item �Ĥν�Ʊ�������ˤ��
����衣
item �Ĥν�Ʊ�������ˤ�� 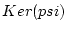 ����Ƴ�����ñ�ͽ�Ʊ��������
�ɤ�ʤ�Τ���(���ξ���˸¤��������ס�)
item
����Ƴ�����ñ�ͽ�Ʊ��������
�ɤ�ʤ�Τ���(���ξ���˸¤��������ס�)
item 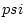 ��
�� 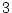 �Ȥǥ桼����åɤθ߽�ˡ��Ԥʤ���
�Ȥǥ桼����åɤθ߽�ˡ��Ԥʤ���
![$ psi(x)=([1]_3,[0]_5,[0]_7)$](img25.png) ��ߤ���
��ߤ��� 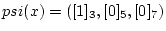 ���ĵ��ʤ�����
item
���ĵ��ʤ�����
item
![$ psi(x)=([1]_3,[2]_5,[3]_7)$](img27.png) ��ߤ���
��ߤ��� 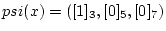 ���ĵ��ʤ�����
item
���ĵ��ʤ�����
item
 �dz���
�dz��� 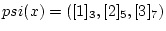 ���ޤꡢ
���ޤꡢ 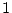 �dz���
�dz��� 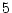 ���ޤꡢ
���ޤꡢ 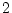 �dz���
�dz���
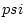 ;��褦���������������3�ĵʤ�����
endenumerate
parendtheorem_type
par
����:
beginitemize
item �������ߤϤʤ�Ǥ�ĤǤ��롣â���̿���ǽ����Ĥ�Τ䡢
¾�ͤ����Ǥˤʤ��Τ������
item �����ѻ汦��ˤ�˺�줺�˳����ֹ��̾������ȡ�
item �����������Ǥ⡢��ʬ������(��ͳ)���Ƥ��ʤ������ˤĤ��Ƥ�
���Ȥ�����Ǥ��äƤ�ۤȤ��ɾ�����ʤ���
enditemize
par
begintheorem_type[q][q][section][definition][][]
mymondaiIendtheorem_type
mymondaiII
mymondaiIII
par
pagebreak
setcounterq0
begintheorem_type[q][q][section][definition][][]
mymondaiIendtheorem_type
par
noindent ����:
par
noindent(1):
beginalign*
6varphi(frac16)
&=
varphi(frac16)
+varphi(frac16)
+varphi(frac16)
+varphi(frac16)
+varphi(frac16)
+varphi(frac16)
;��褦���������������3�ĵʤ�����
endenumerate
parendtheorem_type
par
����:
beginitemize
item �������ߤϤʤ�Ǥ�ĤǤ��롣â���̿���ǽ����Ĥ�Τ䡢
¾�ͤ����Ǥˤʤ��Τ������
item �����ѻ汦��ˤ�˺�줺�˳����ֹ��̾������ȡ�
item �����������Ǥ⡢��ʬ������(��ͳ)���Ƥ��ʤ������ˤĤ��Ƥ�
���Ȥ�����Ǥ��äƤ�ۤȤ��ɾ�����ʤ���
enditemize
par
begintheorem_type[q][q][section][definition][][]
mymondaiIendtheorem_type
mymondaiII
mymondaiIII
par
pagebreak
setcounterq0
begintheorem_type[q][q][section][definition][][]
mymondaiIendtheorem_type
par
noindent ����:
par
noindent(1):
beginalign*
6varphi(frac16)
&=
varphi(frac16)
+varphi(frac16)
+varphi(frac16)
+varphi(frac16)
+varphi(frac16)
+varphi(frac16)
&=varphi(
frac16
+frac16
+frac16
+frac16
+frac16
+frac16
)
=varphi(1)=(1,1,1)
endalign*
�椨�ˡ�
par
noindent(2):
par
noindent(3) (1) ��Ʊ�ͤˤ��ơ�
���狼�롣
�Ƚ�
beginalign*
varphi(p)&=varphi(sum_j p_j X^j)
&=sum_j varphi(p_j) varphi(X)^j
&=sum_j (p_j,p_j,p_j)cdot (1,2,3)^j
&=(sum_j p_j 1^j , sum_j p_j 2^j, sum_j p_j 3^j)
&=(p(1),p(2),p(3))
endalign*
�Ĥޤ�
par
pagebreak
mymondaiII
par
noindent
����:¸�ߤ��ʤ���
par
noindent
��ͳ: �⤷���Τ褦�ʤ�� 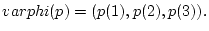 �����ä��Ȥ���ȡ�
�����ä��Ȥ���ȡ�
�Ȥʤä�̷�⤹�뤫�顣
par
mymondaiIII
par
noindent(����):
par
noindent(1):
beginalign*
Ker (psi)
&=psi^-1([0 ]_3,[0]_5,[0]_7)
&={nin Z ;
[n]_3=[0]_3 text ����
[n]_5=[0]_5 text ����
[n]_7=[0]_7
}
&= { nin Z ; nin 3Z text ���� nin 5Z text ���� nin 7Z }
&=3cdot 5cdot 7Z = 105Z
endalign*
par
noindent(2):
noindent(3):
�����Ѥ��롣
��� 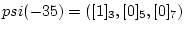 �ϵ����Τΰ�ĤǤ��롣
par
noindent(4):
5 ��
�ϵ����Τΰ�ĤǤ��롣
par
noindent(4):
5 ��
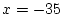 �ȤǸ߽�ˡ��Ԥʤ���
�ȤǸ߽�ˡ��Ԥʤ���
�����롣���Ʊ�ͤˤ���
beginalign*
psi(-35)&=([1]_3,[0]_5,[0]_7)
psi(21)&=([0]_3,[1]_5,[0]_7)
psi(15)&=([0]_3,[0]_5,[1]_7)
endalign*
�롣(�Ǹ�μ���
![$ psi(1)=([1]_3,[1]_5,[1]_7)$](img46.png) �Ⱦ����������롣)
par
beginalign*
&([1]_3,[2]_5,[3]_7)
�Ⱦ����������롣)
par
beginalign*
&([1]_3,[2]_5,[3]_7)
=& 1([1]_3,[0]_5,[0]_7)
+2([0]_3,[1]_5,[0]_7)
+3([0]_3,[0]_5,[1]_7)
=&psi(-35) +2 psi(21)+3psi(15)
=&psi(-35+42+45)=psi(52)
endalign*
par
�椨�� 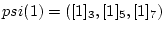 �ϰ�Ĥ���Ǥ��롣
par
noindent(5):
par
�ϰ�Ĥ���Ǥ��롣
par
noindent(5):
par
�ʤɡ�
par
enddocument



Next: About this document ...
2008-01-29