


Next: About this document ...
����� I No.11����
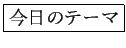 ��ñ�।�ǥ���������Ǹ�ʬ��ĤǤ����
��ñ�।�ǥ���������Ǹ�ʬ��ĤǤ����
����ϡ�ñ�।�ǥ�������(ñ�।�ǥ���Ĥǡ�����ˤ�ʤäƤ����Ρ�
ά����PID)�ϡ�
���ǰ���ʬ��פ�����뤳�Ȥ᤹��
�ޤ���
�Τ褦��̵�Ѥ�ʬ����뤿��ˡ�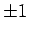 ���ह���Τ����̰�������
���Ȥˤ��롣
���ह���Τ����̰�������
���Ȥˤ��롣
��� 11.1

�ϴĤǤ���Ȥ��롣

�������
�Ѥ˴ؤ��Ʋĵդʤ�Τ����Τ�
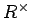
�Ǥ���魯��
��� 11.2
�Ĵ���

�θ�
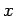
���Ǹ��Ǥ���Ȥϡ�
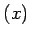
��

���ǥ��ǥ���Ǥ���Ȥ��ˤ�����
�㤨�С�
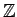 ,
,
![$ {\mathbb{C}}[X]$](img17.png) ���Ǹ�ʬ��ĤǤ��롣��äȰ��̤ˡ�
���Τ��Ȥ�����Ω�ġ�
���Ǹ�ʬ��ĤǤ��롣��äȰ��̤ˡ�
���Τ��Ȥ�����Ω�ġ�
���� 11.1
 ��ñ�।�ǥ�������ʤ�С�
��ñ�।�ǥ�������ʤ�С� ���Ǹ�ʬ��ĤǤ��롣
���Ǹ�ʬ��ĤǤ��롣
���������ξ����Ϥ����Ĥ����ʳ��ˤ狼��롣
�ޤ������λ��¤γ�ĥ����Ϥ���褦��
���� 11.1
���� 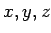 �����äơ�
�����äơ� 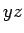 ��
�� 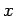 �dz���ڤ졢
����
�dz���ڤ졢
���� 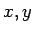 ���ߤ����ǤǤ���Ȥ��롣���ΤȤ���
���ߤ����ǤǤ���Ȥ��롣���ΤȤ���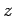 ��
�� 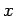 �dz���ڤ�롣
�dz���ڤ�롣
���� 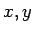 ���ߤ����Ǥʤ顢
���ߤ����Ǥʤ顢
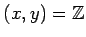 �Ǥ��ä����Ȥ�פ��������ȡ�
��������Ͼ�λ��¤γ�ĥ�Ǥ��뤳�Ȥ�ʬ�����������
�Ǥ��ä����Ȥ�פ��������ȡ�
��������Ͼ�λ��¤γ�ĥ�Ǥ��뤳�Ȥ�ʬ�����������
���� 11.2
�Ĵ���  �θ�
�θ� 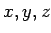 �����äơ�
�����äơ� 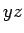 ��
�� 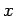 �dz���ڤ졢����
�dz���ڤ졢����
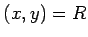 �Ǥ���Ȥ��롣���ΤȤ���
�Ǥ���Ȥ��롣���ΤȤ��� ��
�� 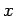 �dz���ڤ�롣
�dz���ڤ�롣
��� 11.4

�ϲĴ��ĤǤ���Ȥ��롣

�θ�
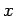
������Ǥ���Ȥϡ�
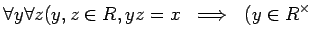
�ޤ���
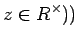
�ΤȤ��˸�����
���� 11.3
 ������Ǥ���Ȥ��롣���ΤȤ���
������Ǥ���Ȥ��롣���ΤȤ���
 ���Ǹ��ϡ�ɬ������Ǥ��롣
���Ǹ��ϡ�ɬ������Ǥ��롣
 �δ��ϡ�ɬ�������Ǹ��Ȥϸ¤�ʤ���
�δ��ϡ�ɬ�������Ǹ��Ȥϸ¤�ʤ���
 ��PID �ʤ����
��PID �ʤ���� �δ���ɬ���Ǹ��Ǥ��롣
�δ���ɬ���Ǹ��Ǥ��롣
�������ˤ�ꡢñ�।�ǥ�������  �θ�
�θ� 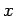 ���ǰ���ʬ�����
���Τ褦�ˤʤ롣
���ǰ���ʬ�����
���Τ褦�ˤʤ롣
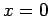 �ޤ���
�ޤ���
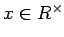 �ʤ�С������ޤ���
�ʤ�С������ޤ���
 ���Ǹ��ʤ�С���Ϥꤪ���ޤ���
���Ǹ��ʤ�С���Ϥꤪ���ޤ���
- ����ʳ��ʤ顢
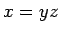 (
(
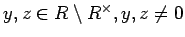 )��
ʬ��Ǥ��롣
)��
ʬ��Ǥ��롣
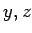 �ˤĤ���Ʊ�ͤΤ��Ȥ롣
(�㤨��
�ˤĤ���Ʊ�ͤΤ��Ȥ롣
(�㤨�� 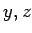 �� �Ǹ��Ǥʤ���С�
�� �Ǹ��Ǥʤ���С� 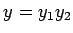 �Ȥʤ롣)
�Ȥʤ롣)
- �����֤���
���Ȥ�����ϡ���Ĥθ���̵�¤�ʬ��Ƥ����ʤ������Ȥ������ȤǤ��롣
������褹��Τˤϡ������������Ѥ���Ф褤��
(����)
![$ {\mathbb{C}}[X]$](img17.png) ����ʬ��
����ʬ��
![$ R={\mathbb{C}}[X^2,X^3]$](img31.png) ��ͤ���ȡ�
��ͤ���ȡ�
![$\displaystyle R=\{f\in {\mathbb{C}}[X];$](img32.png)
$f$ �� $X$ �˴ؤ���켡�ι�η����� $0$
�Ǥ��뤳�Ȥ�ʬ���롣�����ǡ�
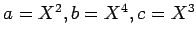 �Ȥ����ȡ�
�Ȥ����ȡ�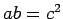 �Ǥ��뤬��
�Ǥ��뤬��
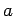 ��
��  �Τʤ��Ǵ���Ǥ���
�Τʤ��Ǵ���Ǥ���
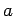 ��
��  �Τʤ���
�Τʤ��� 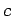 ������ǤϤʤ���
������ǤϤʤ���
�Ȥ������Ȥ�ʬ���롣���Τ褦�ˡ�ñ�ˡִġפȤ��äƤ⤳�Τ褦�ʡ��ðۤʡ״Ĥ�
�ޤޤ��Τǡ����θ��μ�갷���ˤ��̾���������갷���ʾ�����դ�ɬ�פǤ��롣
![% latex2html id marker 1190
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{5}] $](img37.png) �Τʤ���
�Τʤ���
�ʤɤ⡢�ǰ���ʬ�������������Ǥ��롣
����ݡ�������
�Ĥ��Τ�����������Ʋʤ�����
(���¡����ιֵ��ν�λ���ޤǡ�)
- (I).
- ����
 ���Ф��ơ����Τ��Ȥ��ʤ�����
���Ф��ơ����Τ��Ȥ��ʤ�����
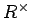 �Ͼ�ˡ�˴ؤ��Ʒ���ʤ���
�Ͼ�ˡ�˴ؤ��Ʒ���ʤ���
 �˼��Τ褦��Ʊ�ʹط���뤳�Ȥ�����롣
�˼��Τ褦��Ʊ�ʹط���뤳�Ȥ�����롣
(����Ʊ�ʹط���Ʊ�ͤ���Ĥθ���Ʊȼ����Ĥθ��ȸƤ֡�)
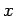 ��
�� 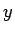 ���ܸ��ǡ�
���ܸ��ǡ�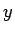 ��
�� 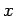 ���ܸ��Ǥ⤢��ʤ顢
���ܸ��Ǥ⤢��ʤ顢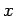 ��
�� 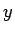 �Ȥ�
Ʊȼ�Ǥ��롣
�Ȥ�
Ʊȼ�Ǥ��롣
- (II).
- ����
 ��Ϳ�����Ƥ���Ȥ���
��Ϳ�����Ƥ���Ȥ���
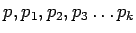 ������
������  ���Ǹ��Ǥ���Ȥ��롣���ΤȤ����⤷
���Ǹ��Ǥ���Ȥ��롣���ΤȤ����⤷
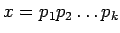 ��
��
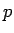 ���ܸ��Ǥ���С�
���ܸ��Ǥ���С�
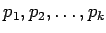 �Τ����ɤ줫��Ĥ�ɬ��
�Τ����ɤ줫��Ĥ�ɬ��
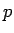 ��Ʊȼ�Ǥ��뤳�Ȥ��ʤ�����(Ʊȼ����������仲�ȡ�â����
����������뤳�Ȥ��ᤷ�ʤ���(����η�̤ϲ��ꤷ�Ƥ褤��))
��Ʊȼ�Ǥ��뤳�Ȥ��ʤ�����(Ʊȼ����������仲�ȡ�â����
����������뤳�Ȥ��ᤷ�ʤ���(����η�̤ϲ��ꤷ�Ƥ褤��))
- (III).
-
![% latex2html id marker 1230
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{-1}]$](img47.png) �ϥ桼����åɴġ��������ä��Ǹ�ʬ��ĤǤ��롣(��������)
�����ǡ�
�ϥ桼����åɴġ��������ä��Ǹ�ʬ��ĤǤ��롣(��������)
�����ǡ�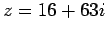 ��
��
![% latex2html id marker 1234
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{-1}]$](img49.png) �ˤ������Ǹ�ʬ�衣
(�ҥ��: �ޤ�
�ˤ������Ǹ�ʬ�衣
(�ҥ��: �ޤ� 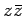 ���ǰ���ʬ����ߤ衣�ǰ���ʬ��ΰ��������С�
������ʿ��ζ��̰����������ʤ�Ȧ�Ǥ��롣
���������Ȥ��ϥ桼����åɤθ߽�ˡ���Ѥ��衣�Ǹ�ˡ�
�����������Ǹ��Ǥ��뤫�ɤ����Τꤿ���Ȥ��ˤϡ�
���ǰ���ʬ����ߤ衣�ǰ���ʬ��ΰ��������С�
������ʿ��ζ��̰����������ʤ�Ȧ�Ǥ��롣
���������Ȥ��ϥ桼����åɤθ߽�ˡ���Ѥ��衣�Ǹ�ˡ�
�����������Ǹ��Ǥ��뤫�ɤ����Τꤿ���Ȥ��ˤϡ�
�Ȥ������Ȥޤ��Ѥ��衣
)



Next: About this document ...
2007-12-12
![]() ��ñ�।�ǥ���������Ǹ�ʬ��ĤǤ����
��ñ�।�ǥ���������Ǹ�ʬ��ĤǤ����
![]() ,
,
![]() ���Ǹ�ʬ��ĤǤ��롣��äȰ��̤ˡ�
���Τ��Ȥ�����Ω�ġ�
���Ǹ�ʬ��ĤǤ��롣��äȰ��̤ˡ�
���Τ��Ȥ�����Ω�ġ�
![]() �θ�
�θ� ![]() ���ǰ���ʬ�����
���Τ褦�ˤʤ롣
���ǰ���ʬ�����
���Τ褦�ˤʤ롣
![]() ����ʬ��
����ʬ��
![]() ��ͤ���ȡ�
��ͤ���ȡ�
![]() �Τʤ���
�Τʤ���