


: ïŋ―ïŋ―ïŋ―ïŋ―Ęļïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―...
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― I No.7ïŋ―ïŋ―ïŋ―ïŋ―
 ïŋ―ÔīÄĪÎ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―ïŋ―
ïŋ―ÔīÄĪÎ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―ïŋ―
ïŋ―ïŋ― 7.1 (ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îīïŋ―ïŋ―ïŋ―ïŋ―ïŋ―1)
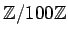
ïŋ―ïŋ―ïŋ―ïŋ―
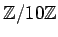
ïŋ―ØĪΞïŋ―ïŋ―ïŋ―

ïŋ―ïŋ―
![% latex2html id marker 1091
$\displaystyle f([n]_{100})=[n]_{10} \quad \quad ($](img5.png)
$[?]_n$ ïŋ―ïŋ― $$
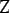
$/n$
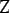
$$ ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
$?$ ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―
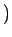
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ―ĘŽïŋ―ïŋ―ïŋ―ëĄĢ
 ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―
 ïŋ―ÏīÄĪÎ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ÏīÄĪÎ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
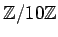 ïŋ―ïŋ―ïŋ―ÎĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ÎĪĮĪïŋ―ïŋ―ëĄĢ
 ïŋ―ÎģËĪïŋ―
ïŋ―ÎģËĪïŋ―
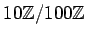 ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ÃĪÆĄïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ęĄĒ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ― 7.2
ïŋ―ÄĪČĪïŋ―ïŋ―ÆĪïŋ―Æąïŋ―ïŋ―
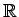
![$ [X]/(X^2+1)$](img11.png)
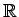
![$ [X] \cong {\mathbb{C}}$](img12.png)
ïŋ―ïŋ―
Âļïŋ―ßĪïŋ―ïŋ―ëĄĢ
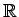
![$ [X]$](img13.png)
ïŋ―ïŋ―ïŋ―ïŋ―
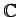
ïŋ―ØĪΞïŋ―ïŋ―ïŋ―

ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ―ĘŽïŋ―ïŋ―ïŋ―ëĄĢ
 ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢ
ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢ
 ïŋ―ÏīÄĪÎ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ÏīÄĪÎ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
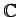 ïŋ―ïŋ―ïŋ―ÎĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ÎĪĮĪïŋ―ïŋ―ëĄĢ
 ïŋ―ÎģËĪïŋ―
ïŋ―ÎģËĪïŋ―
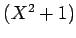
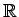
![$ [X]$](img13.png) ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ÃĪÆĄïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ęĄĒ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ― 7.3 (ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îąïŋ―ïŋ―ïŋ―ïŋ―ãĢą)
![$ {\mbox{${\mathbb{Z}}$}}[X]$](img20.png)
ïŋ―ïŋ―ïŋ―ïŋ―
![% latex2html id marker 1149
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{14}]$](img21.png)
ïŋ―ØĪΞïŋ―ïŋ―ïŋ―

ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ―ĘŽïŋ―ïŋ―ïŋ―ëĄĢ
 ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![% latex2html id marker 1159
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{14}]$](img23.png) ïŋ―ïŋ―ïŋ―ïŋ―ÏĪß―ÐĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÏĪß―ÐĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―
 ïŋ―ÏīÄĪÎ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ÏīÄĪÎ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![% latex2html id marker 1165
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{14}]$](img24.png) ïŋ―ïŋ―ïŋ―ÎĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ÎĪĮĪïŋ―ïŋ―ëĄĢ
 ïŋ―ÎģËĪïŋ―
ïŋ―ÎģËĪïŋ―
![$ (X^2-14){\mbox{${\mathbb{Z}}$}}[X]$](img25.png) ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ÃĪÆĄïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ęĄĒ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ― 7.4 (ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îąïŋ―ïŋ―ïŋ―ïŋ―ãĢē)
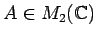
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―áĄĒ
![$ {\mathbb{C}}[X]$](img29.png)
ïŋ―ïŋ―ïŋ―ïŋ―
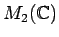
ïŋ―ØĪΞïŋ―ïŋ―ïŋ―

ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ―ĘŽïŋ―ïŋ―ïŋ―ëĄĢ
 ïŋ―ÏīÄĪÎ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ÏīÄĪÎ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
 ïŋ―ÎģËĪïŋ―
ïŋ―ÎģËĪïŋ―
![$ (X^2-8 X-8){\mathbb{C}}[X]$](img33.png) ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ÃĪÆĄïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ęĄĒ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ÝĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÄĪïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ōĪ·ĪÆēōĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ïŋ―ÂĄïŋ―ïŋ―ïŋ―ïŋ―ÎđÖĩïŋ―ïŋ―Î―ïŋ―Îŧïŋ―ïŋ―ïŋ―ÞĪĮĄïŋ―)
- (I).
-
ïŋ―ïŋ―
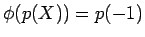 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÏĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÏĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
-
ïŋ―ïŋ―
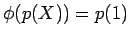 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―ČĪïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÏĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―ČĪïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÏĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
- (II).
-
ïŋ―ōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―



: ïŋ―ïŋ―ïŋ―ïŋ―Ęļïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―...
Ęŋïŋ―ïŋ―19ĮŊ11ïŋ―ïŋ―29ïŋ―ïŋ―
![]() ïŋ―ÔīÄĪÎ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―ïŋ―
ïŋ―ÔīÄĪÎ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―ïŋ―
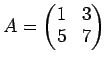
![$\displaystyle {\mathbb{C}}[A]=
{\mathbb{C}}A+{\mathbb{C}}E= \{k A+ lE ; k,l \in...
...in{pmatrix}
k+l &3k \\
5k &7k+l
\end{pmatrix}; k,l \in {\mathbb{C}}
\right \}
$](img32.png)