 пњљќ§»§пњљпњљпњљ
пњљќ§»§пњљпњљпњљ
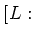
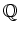
![$ ]$](img11.png) пњљпњљпњљпњљи°£
пњљпњљпњљпњљи°£
-
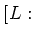
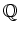
![$ ]=2$](img12.png) пњљ §пњљ
пњљ §пњљ 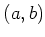 пњљпњљ2пњљ»µпњљб°Ґпњљпњљпњљќ§»§пњљпњљпњљ
пњљпњљ2пњљ»µпњљб°Ґпњљпњљпњљќ§»§пњљпњљпњљ 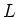 пњљпњљ
пњљпњљпњљм§Њпњљпњљпњљпњљи°£
пњљпњљ
пњљпњљпњљм§Њпњљпњљпњљпњљи°£
пњљпњљпњљпњљ:
(1)
![]()
![]()
![]() пњљ»§пњљпњљпњљпњљпњљ
пњљ»§пњљпњљпњљпњљпњљ
![]() пњљ«§пњљпњљ√§∆°пњљпњљ §пњљпњљпњљпњљпњљ
пњљ«§пњљпњљ√§∆°пњљпњљ §пњљпњљпњљпњљпњљ
![]()
![]()
![]() пњљ«§пњљпњљл§≥пњљ»§тЉ®§пњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљ«§пњљпњљл§≥пњљ»§тЉ®§пњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљ«§пњљпњљл§≥пњљ»§пњљпњљп§Ђпњљл°£
Part 0)пњљё§пњљпњљƒ§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ∆§пњљпњљпњљпњљпњљ
пњљ §пњљпњљ
пњљ»љс§±§л°£ќЊпњљ’§пњљпњљпњљи§єпњљпњљпњљ
пњљпњљпњљпњљЋ§пњљк°Ґ
пњљ»§пњљпњљпњљ пњљпњљ‘§ќЉпњљпњљпњљпњљпњљ
(i) ![]() пњљќЊпњљз°£
пњљќЊпњљз°£
пњљпњљпњљ §пњљпњљ
пњљпњљпњљ §к§њпњљƒ°пњљпњљпњљпњљпњљпњљ
(ii) ![]() пњљќЊпњљз°£
пњљќЊпњљз°£
пњљпњљпњљ §к§њпњљƒ°пњљпњљпњљпњљпњљпњљ
пњљ…§ќЊпњљпњљпњљћЈпњљв§ђпњљпњљпњљпњљпњљпњљпњљпњљпњљй°Ґпњљпњљпњљк§ђпњљпњљпњљпњљпњљпњљпњљпњљпњљ»§пњљпњљпњљпњљпњљпњљпњљпњљм§њпњљпњљпњљ»§Ћ§ §л°£
![]()
Part I)
![]()
![]()
![]() 觶Ћ§пњљ
觶Ћ§пњљ
пњљ §пњљпњљпњљ ђпњљќ§пњљпњљпњљпњљЌ§пњљпњљ∆°пњљпњљ∆•пњљпњљ∆•√•„§«§ќ≥пњљпњљзЉ°пњљпњљпњљпњљ∆°пњљпњљпњљпњљпњљпњљпњљ…§пњљпњљпњљ пњљпњљпњљм§Њпњљпњљќ•пњљпњљ∆•√•„§«§ѕ°пњљ њпњљпњљпњљпњљпњљпњљпњљƒ§пњљпњљпњљпњљ’§пњљпњљ√§пњљпњљ∆§пњљпњљпњљќ§«§пњљпњљл§Ђпњљй°Ґ пњљпњљпњљзЉ°пњљпњљпњљпњљ2пњљпњљпњљпњљпњљё§пњљпњљпњљ 1пњљпњљпњљпњљпњљпњљпњљпњљпњљз§Јпњљ∆§пњљпњљ §пњљ)пњљпњљпњљќ§пњљпњљпњљпњљм§Ђпњљ«§пњљпњљл°£
пњљ÷µпњљпњљ«љ“§ў§пњљпњљи§¶пњљЋ°пњљ![]() пњљпњљЌ≠пњљпњљпњљпњљпњљ«§ §пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ√§∆°пњљ
пњљпњљЌ≠пњљпњљпњљпњљпњљ«§ §пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ√§∆°пњљ
пњљƒ§пњљпњљЋ°пњљ
![]() пњљќ§пњљпњљпњљпњљпњљпњљ
пњљќ§пњљпњљпњљпњљпњљпњљ
![]() пњљќЄпњљпњљ«§ §пњљпњљпњљпњљ»§пњљпњљй°Ґпњљпњљпњљпњљпњљпњљ—§пњљпњљ∆°пњљ
пњљќЄпњљпњљ«§ §пњљпњљпњљпњљ»§пњљпњљй°Ґпњљпњљпњљпњљпњљпњљ—§пњљпњљ∆°пњљ
![]()
![]() пњљпњљпњљп§Ђпњљл°£пњљж§®пњљЋ°пњљ
пњљпњљпњљп§Ђпњљл°£пњљж§®пњљЋ°пњљ
пњљпњљпњљпњљЋ°пњљ
![]()
![]()
![]() пњљ«§пњљпњљл°£пњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљЋ°пњљ«°пњљ
пњљ«§пњљпњљл°£пњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљЋ°пњљ«°пњљ
![]()
![]()
![]() пњљ»≤пњљпњљк§єпњљпњљ»°пњљпњљпњљпњљпњљпњљ
пњљ»≤пњљпњљк§єпњљпњљ»°пњљпњљпњљпњљпњљпњљ
![]()
![]()
![]() пњљќЊпњљпњљЋ§пњљпњљпњљпњљпњљ∆°пњљ
пњљќЊпњљпњљЋ§пњљпњљпњљпњљпњљ∆°пњљ
![]() пњљпњљ
пњљпњљпњљпњљпњљм§Ђпњљпњљ
пњљпњљ
пњљпњљпњљпњљпњљм§Ђпњљпњљ
![]()
![]() пњљпњљ¬∞пњљпњљпњљЌ§–§ §пњљ §пњљпњљ §л°£пњљ∆§пњљпњљпњљпњљпњљпњљ
(пњљпњљпњљў§пњљ
пњљпњљ¬∞пњљпњљпњљЌ§–§ §пњљ §пњљпњљ §л°£пњљ∆§пњљпњљпњљпњљпњљпњљ
(пњљпњљпњљў§пњљ
![]()
![]() пњљ»§пњљпњљпњљ)пњљпњљпњљпњљпњљпњљпњљ»°пњљ
пњљ»§пњљпњљпњљ)пњљпњљпњљпњљпњљпњљпњљ»°пњљ
пњљќ§пњљпњљпњљпњљм§Ђпњљпњљ
пњљпњљ√§∆°пњљ
пњљпњљпњљ
![]()
![]() пњљпњљ
пњљпњљ
![]() пњљпњљќ•ў•пњљпњљ»•пњљпњљпњљ÷§»§пњљпњљпњљ
пњљпњљќ•ў•пњљпњљ»•пњљпњљпњљ÷§»§пњљпњљпњљ
пњљпњљ
Part II)
![]()
![]()
![]() 觶
觶
![]() пњљпњљ
пњљпњљ
![]() пњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљпњљпњљпњљпњљ
![]() пњљпњљ
пњљпњљпњљпњљѕ§пњљпњљм§Њпњљпњљ
пњљпњљ
пњљпњљпњљпњљѕ§пњљпњљм§Њпњљпњљ ![]() пњљќ§ §пњљпњљпњљ¬Єпњљя§пњљпњљпњљќ§«°пњљ
пњљќ§ §пњљпњљпњљ¬Єпњљя§пњљпњљпњљќ§«°пњљ![]() пњљпњљ
пњљпњљ
![]() пњљпњљ
Ќ≠пњљ¬Љпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљз°Ґпњљпњљпњљ §пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
пњљпњљ
Ќ≠пњљ¬Љпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљз°Ґпњљпњљпњљ §пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
![]()
![]()
![]() пњљќЄпњљпњљпњљ
пњљќЄпњљпњљпњљ
![]() пњљпњљ
пњљ∆°пњљпњљќє‘§пњљпњљпњљ(пњљпњљпњљм§Њпњљпњљпњљпњљпњљћ§пњљ)пњљпњљпњљпњљ∆§пњљпњљ»Јпњљё§к°Ґпњљв°є 8пњљƒ§пњљпњљпњљпњљ §пњљпњљпњљ
пњљпњљ
пњљ∆°пњљпњљќє‘§пњљпњљпњљ(пњљпњљпњљм§Њпњљпњљпњљпњљпњљћ§пњљ)пњљпњљпњљпњљ∆§пњљпњљ»Јпњљё§к°Ґпњљв°є 8пњљƒ§пњљпњљпњљпњљ §пњљпњљпњљ
¬Њпњљпњљпњљ«°пњљ
![]()
![]()
![]()
![]()
![]() пњљ«§пњљпњљл§Ђпњљй°Ґпњљпњљ…Њеµ≠пњљпњљ«љпњљпњљпњљпњљ
пњљпњљпњљў§∆§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќЄпњљпњљ»§пњљпњљ∆µпњљпњљпњљпњљпњљл§≥пњљ»§Ћ§ §л°£пњљпњљпњљ §пњљпњљпњљпњљ
пњљ«§пњљпњљл§Ђпњљй°Ґпњљпњљ…Њеµ≠пњљпњљ«љпњљпњљпњљпњљ
пњљпњљпњљў§∆§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќЄпњљпњљ»§пњљпњљ∆µпњљпњљпњљпњљпњљл§≥пњљ»§Ћ§ §л°£пњљпњљпњљ §пњљпњљпњљпњљ
![]() пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
пњљЋ§пњљпњљпњљпњљпњљпњљ∆°пњљ
![]()
![]()
![]() пњљпњљ
пњљпњљ
Part III) ![]() 򊮧
򊮧
![]() пњљпњљ
пњљпњљ
![]() .
пњљЋЇпњљпњљ—§пњљпњљпњљпњљпњљ»°пњљ
.
пњљЋЇпњљпњљ—§пњљпњљпњљпњљпњљ»°пњљ
Part I) пњљќЇ«Єпњљпњљпњљпњљпњљ’§пњљпњљпњљпњљи§¶пњљЋ°пњљ
пњљпњљпњљп§Ђпњљл°£пњљ»§пњљпњљЋ°пњљ
(2)
пњљ«§пњљпњљл§Ђпњљй°Ґ
пњљ«§пњљпњљл°£
(пњљпњљ)
![]() , пњљпњљпњљ §пњљпњљ
, пњљпњљпњљ §пњљпњљ
![]() пњљќ§»§пњљпњљпњљ
пњљќ§»§пњљпњљпњљ
пњљпњљпњљќ§»§пњљпњљпњљ
![]()
![]()
![]()
![]() пњљ«§пњљпњљл°£
пњљ«§пњљпњљл°£
(пњљпњљ)
![]() , пњљпњљпњљ §пњљпњљ
, пњљпњљпњљ §пњљпњљ
![]() пњљќ§»§пњљпњљпњљ
пњљќ§»§пњљпњљпњљ
пњљпњљпњљќ§»§пњљпњљпњљ
![]()
![]()
![]()
![]() пњљ«§пњљпњљл°£
пњљ«§пњљпњљл°£
(пњљпњљ)
![]() , пњљпњљпњљ §пњљпњљ
, пњљпњљпњљ §пњљпњљ
![]() пњљќ§»§пњљпњљпњљ
пњљќ§»§пњљпњљпњљ
пњљпњљпњљќ§»§пњљпњљпњљ
![]()
![]()
![]()
![]() пњљ«§пњљпњљл°£
пњљ«§пњљпњљл°£