


Next: About this document ...
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝIII ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ No.11
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮฅฦก๏ฟฝ๏ฟฝ๏ฟฝ

๏ฟฝ๏ฟฝ๏ฟฝ 11.1
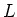
๏ฟฝ๏ฟฝ
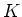
๏ฟฝฮฅ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮคศค๏ฟฝ๏ฟฝ๏ฟฝ
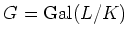
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝสฌ๏ฟฝ๏ฟฝ
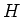
๏ฟฝ๏ฟฝ๏ฟฝะค๏ฟฝ๏ฟฝฦก๏ฟฝ
๏ฟฝศค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
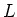
๏ฟฝ๏ฟฝ
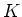
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮควค๏ฟฝ๏ฟฝ๋กฃ
๏ฟฝฤค๏ฟฝ๏ฟฝฮค๏ฟฝ๏ฟฝศคฯค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝหค๏คซ๏ฟฝ๋กฃ
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ 11.1
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮฒ๏ฟฝ๏ฟฝ๏ฟฝฮค๏ฟฝศควก๏ฟฝ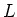 ๏ฟฝ๏ฟฝ
๏ฟฝ๏ฟฝ 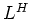 ๏ฟฝฮฅ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝวค๏ฟฝ๏ฟฝ๋กฃ
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝหก๏ฟฝ
๏ฟฝฮฅ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝวค๏ฟฝ๏ฟฝ๋กฃ
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝหก๏ฟฝ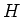 ๏ฟฝฯผ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
๏ฟฝฯผ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
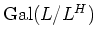 ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝสฌ๏ฟฝ๏ฟฝ๏ฟฝศค฿คสค๏ฟฝ๏ฟฝ๋กฃ
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝสฌ๏ฟฝ๏ฟฝ๏ฟฝศค฿คสค๏ฟฝ๏ฟฝ๋กฃ
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝืคสป๏ฟฝ๏ฟฝยคฯก๏ฟฝ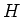 ๏ฟฝ๏ฟฝ๏ฟฝยค๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝยค๏ฟฝ
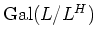 ๏ฟฝศฐ๏ฟฝ๏ฟฝืค๏ฟฝ๏ฟฝ๋คณ๏ฟฝศควค๏ฟฝ๏ฟฝ๋กฃ
(๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ 11.1.)
๏ฟฝ๏ฟฝ๏ฟฝฮค๏ฟฝ๏ฟฝ๏ฟฝหคฤค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝัค๏ฟฝ๏ฟฝ๋กฃ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝหคฯก๏ฟฝ
๏ฟฝศฐ๏ฟฝ๏ฟฝืค๏ฟฝ๏ฟฝ๋คณ๏ฟฝศควค๏ฟฝ๏ฟฝ๋กฃ
(๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ 11.1.)
๏ฟฝ๏ฟฝ๏ฟฝฮค๏ฟฝ๏ฟฝ๏ฟฝหคฤค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝัค๏ฟฝ๏ฟฝ๋กฃ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝหคฯก๏ฟฝ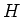 ๏ฟฝหค๏ฟฝ๏ฟฝ๏ฟฝะพฮฒ๏ฟฝ(สฟ๏ฟฝัฒ๏ฟฝ)๏ฟฝืค๏ฟฝ
๏ฟฝฦฅ๏ฟฝ๏ฟฝหฅรฅ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝัค๏ฟฝ๏ฟฝ๋กฃ
๏ฟฝหค๏ฟฝ๏ฟฝ๏ฟฝะพฮฒ๏ฟฝ(สฟ๏ฟฝัฒ๏ฟฝ)๏ฟฝืค๏ฟฝ
๏ฟฝฦฅ๏ฟฝ๏ฟฝหฅรฅ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝัค๏ฟฝ๏ฟฝ๋กฃ
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ 11.2
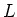 ๏ฟฝ๏ฟฝ
๏ฟฝ๏ฟฝ 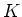 ๏ฟฝฮฅ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝวค๏ฟฝ๏ฟฝ๏ฟฝศค๏ฟฝ๏ฟฝ๋กฃ
วค๏ฟฝีค๏ฟฝ
๏ฟฝฮฅ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝวค๏ฟฝ๏ฟฝ๏ฟฝศค๏ฟฝ๏ฟฝ๋กฃ
วค๏ฟฝีค๏ฟฝ 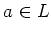 ๏ฟฝ๏ฟฝ
๏ฟฝ๏ฟฝ
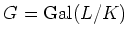 ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝสฌ๏ฟฝ๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝสฌ๏ฟฝ๏ฟฝ 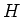 ๏ฟฝ๏ฟฝ๏ฟฝะค๏ฟฝ๏ฟฝฦก๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝะค๏ฟฝ๏ฟฝฦก๏ฟฝ
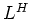 -๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮฅ๏ฟฝหฅรฅ๏ฟฝ๏ฟฝ๏ฟฝยฟ๏ฟฝเผฐ
-๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮฅ๏ฟฝหฅรฅ๏ฟฝ๏ฟฝ๏ฟฝยฟ๏ฟฝเผฐ 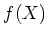 ๏ฟฝวก๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮค๏ฟฝยธ๏ฟฝ฿ค๏ฟฝ๏ฟฝ๋กฃ
๏ฟฝวก๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮค๏ฟฝยธ๏ฟฝ฿ค๏ฟฝ๏ฟฝ๋กฃ
-
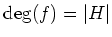
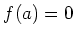
๏ฟฝ๏ฟฝ 11.1
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮฒ๏ฟฝ๏ฟฝ๏ฟฝฮค๏ฟฝศควก๏ฟฝ
![% latex2html id marker 798
$ [L:L^H]\leq \vert H\vert$](img13.png) .
.
๏ฟฝ๏ฟฝ๏ฟฝฮทฯค๏ฟฝ๏ฟฝ๏ฟฝฤพ๏ฟฝ๏ฟฝ๏ฟฝหก๏ฟฝ๏ฟฝ๏ฟฝแคฟ๏ฟฝ๏ฟฝ๏ฟฝรค๏ฟฝ๏ฟฝฤค๏ฟฝ๏ฟฝฮค๏ฟฝ๏ฟฝศค๏ฟฝ๏ฟฝ๏คซ๏ฟฝ๋กฃ
2006-12-14
![]()
![]() ๏ฟฝ๏ฟฝ๏ฟฝยค๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝยค๏ฟฝ
![]() ๏ฟฝศฐ๏ฟฝ๏ฟฝืค๏ฟฝ๏ฟฝ๋คณ๏ฟฝศควค๏ฟฝ๏ฟฝ๋กฃ
(๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ 11.1.)
๏ฟฝ๏ฟฝ๏ฟฝฮค๏ฟฝ๏ฟฝ๏ฟฝหคฤค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝัค๏ฟฝ๏ฟฝ๋กฃ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝหคฯก๏ฟฝ
๏ฟฝศฐ๏ฟฝ๏ฟฝืค๏ฟฝ๏ฟฝ๋คณ๏ฟฝศควค๏ฟฝ๏ฟฝ๋กฃ
(๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ 11.1.)
๏ฟฝ๏ฟฝ๏ฟฝฮค๏ฟฝ๏ฟฝ๏ฟฝหคฤค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝัค๏ฟฝ๏ฟฝ๋กฃ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝหคฯก๏ฟฝ![]() ๏ฟฝหค๏ฟฝ๏ฟฝ๏ฟฝะพฮฒ๏ฟฝ(สฟ๏ฟฝัฒ๏ฟฝ)๏ฟฝืค๏ฟฝ
๏ฟฝฦฅ๏ฟฝ๏ฟฝหฅรฅ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝัค๏ฟฝ๏ฟฝ๋กฃ
๏ฟฝหค๏ฟฝ๏ฟฝ๏ฟฝะพฮฒ๏ฟฝ(สฟ๏ฟฝัฒ๏ฟฝ)๏ฟฝืค๏ฟฝ
๏ฟฝฦฅ๏ฟฝ๏ฟฝหฅรฅ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝัค๏ฟฝ๏ฟฝ๋กฃ