


Next: Elementary category theory
Up: Topics in Non commutative
Previous: locally free sheaves of
DEFINITION 4.1
A set

of subsets of a set
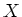
is called
a
filter on
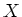
if the following conditions are
satisfied.
-
 .
.
-
 .
.
DEFINITION 4.2
A maximal filter on a set
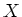
is called an
ultra filter on
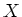
.
Those readers who are not familiar with the arguments are invited to read
for example [15] or the book of Bourbaki [2].
LEMMA 4.3
Let
 be a filter on a set
be a filter on a set 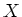 The following statements are equivalent.
The following statements are equivalent.
-
 is an ultrafilter. That means, a maximal filter.
is an ultrafilter. That means, a maximal filter.
- for any subset
 , we have either
, we have either
 or
or

DEFINITION 4.4
A principal filter on a set
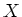
is an ultra filter of the form

where

is an element of
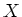
.
A ultrafilter which is not principal filter is called non-principal.
An ultrafilter
 on a set
on a set 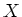 may
be identified with a point
of Stone-Cech compactification of (
may
be identified with a point
of Stone-Cech compactification of (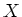 with discrete topology).
A non principal ultrafilter is identified with a
boundary point.
with discrete topology).
A non principal ultrafilter is identified with a
boundary point.
DEFINITION 4.6
Let

be a number field with the ring
of integers

.
Let

be a non-principal ultrafilter on the set

of all primes of

of height 1.
Let
 be an ideal of
be an ideal of
 defined as follows:
defined as follows:
Then we define a ring

as follows:
We denote by

the canonical projection from

to

.
PROOF..
Indeed, let

be a non zero element in

.
Let

.
Then for any

,
intersection

is non empty.
Maximality of

now implies that

itself is a member of

.
The inverse

of
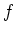
in

is given by the following formula.
If

in

for a positive integer
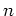
,
then there exists

such that

. On the other hand,
as we have mentioned in Lemma
4.5 above,
being a member of a non-principal filter

,

cannot be a finite set.
This is a contradiction,
since non-zero member
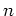
in

has only finite ``zeros'' on
the ``arithmetic curve''

.
Thus the characteristic of

is zero.
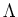
The definition above is partly inspired by works of
Kirchberg (See [12] for example.)
We would like to give a
little explanation on
 . We regard it as a kind of `limit'.
If we are given a member
. We regard it as a kind of `limit'.
If we are given a member 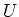 of
of
 and
we have an element, say,
and
we have an element, say,
 of
of
 for each primes
for each primes
 , then, by assigning
arbitrary element to `exceptional' primes (that means, primes which
are not in
, then, by assigning
arbitrary element to `exceptional' primes (that means, primes which
are not in 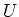 ), we may interpolate
), we may interpolate  and
consider
and
consider
The element ('limit') does not actually depend on
the interpolation. Thus we may refer to the element without specifying the
interpolation. In particular, this applies to the case where we have
 for almost all primes
for almost all primes
 .
The same type of argument applies for polynomials. We summarize this in the
following Lemma.
.
The same type of argument applies for polynomials. We summarize this in the
following Lemma.
LEMMA 4.8
Suppose we have a co-finite subset 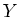 of
of
 and a collection
and a collection
![$ \{F_\mathfrak{p}\}_{\mathfrak{p}\in Y} \in
(\mathfrak{O}/\mathfrak{p})[T_1,T_2,\dots,T_n,U_1,U_2,\dots,U_n]$](img87.png) of polynomials. Assume we have a bound
of polynomials. Assume we have a bound  for the degrees of the polynomials.
That means,
for the degrees of the polynomials.
That means,
Then we may define the `limit'
by taking `limit' of each of the coefficients.
The same arguments also applies for polynomial maps.
For any non-principal ultra filter
 on
on
 (prime numbers)
,
We may consider the following ring.
(prime numbers)
,
We may consider the following ring.

$U$ �� $0$
It turns out that,
Thus we conclude that
PROPOSITION 4.10
As an abstract field,



Next: Elementary category theory
Up: Topics in Non commutative
Previous: locally free sheaves of
2007-12-11
 .
.
 .
.
![]() on a set
on a set ![]() may
be identified with a point
of Stone-Cech compactification of (
may
be identified with a point
of Stone-Cech compactification of (![]() with discrete topology).
A non principal ultrafilter is identified with a
boundary point.
with discrete topology).
A non principal ultrafilter is identified with a
boundary point.
![]() be an ideal of
be an ideal of
![]() defined as follows:
defined as follows:



![]()
![]() . We regard it as a kind of `limit'.
If we are given a member
. We regard it as a kind of `limit'.
If we are given a member ![]() of
of
![]() and
we have an element, say,
and
we have an element, say,
![]() of
of
![]() for each primes
for each primes
![]() , then, by assigning
arbitrary element to `exceptional' primes (that means, primes which
are not in
, then, by assigning
arbitrary element to `exceptional' primes (that means, primes which
are not in ![]() ), we may interpolate
), we may interpolate ![]() and
consider
and
consider
![]() on
on
![]() (prime numbers)
,
We may consider the following ring.
(prime numbers)
,
We may consider the following ring.
 $U$ �� $0$
$U$ �� $0$