morphism of finite type

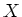
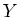
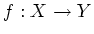
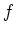
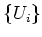
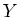
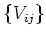
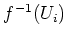
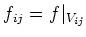
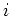
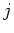
DEFINITION 10.1   Let $X$ , $Y$ be schemes, and let $f:X\to Y$ be a morphism. We say that $f$ is of finite type if there exists an open cover $\{U_i\}$ of $Y$ by affine schemes and a finite open cover $\{V_{i j}\}$ of each $f^{-1}(U_i)$ by affine schemes such that $f_{i j}= f\vert _{V_{i j}}$ is ``a morphism of finite type'' for every $i$ and $j$ . That means, if we put

$$\Gamma_{f_{i j}}: A_i=\Gamma(\mathcal{O}_{U_i}) \to \Gamma(\mathcal{O}_{V_{i j}}) =B_{i j}$$

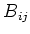
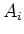
Then $B_{i j}$ is finitely generated algebra over $A_{i}$ .