


Next: derivations
Up: differential calculus of schemes
Previous: local description of differential
Let 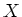 be a separated
be a separated 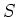 -scheme.
For each
-scheme.
For each
 , there exists a natural projection map.
, there exists a natural projection map.
Let us restrict ourselves to the case where  .
.
 is equal to
is equal to
 and
and  splits in
a natural way.
splits in
a natural way.

split
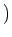
which yields an decomposition
for a unique quasi coherent sheaf
 .
.
DEFINITION 9.15
The sheaf

is
called the
sheaf of 1-forms on
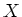
relative to
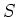
.
Subsections
2007-12-11