DEFINITION 8.1
Let
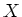
be a scheme. Let
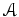
be a quasi coherent sheaf with an
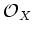
-bilinear multiplication so that
it is a sheaf of (unital associative) algebras.
Then we may construct a scheme
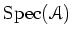
over
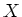
.
The morphism
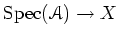
is called an
explicit affine morphism.
A morphism which is isomorphic to an explicit
affine morphism so defined is called an
affine morphism.