a sequence
is also exact.
a sequence
is also exact.
Note that we have the following
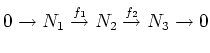
of
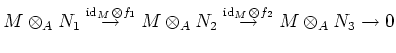
is also exact. Thus
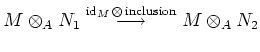
is injective.
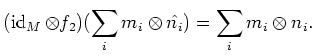
Thus the map
Thus
On the other hand, for any element
We may easily check that
Then it is easy to show that the homomorphisms
(See for example [14, Appendix A] or [1].)
![]()
A morphism of affine schemes is flat if the corresponding ring homomorphism is flat.
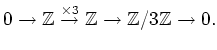
Then by tensoring with
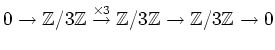
which is not exact.
Let us view it as a homomorphism
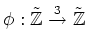 of quasi coherent sheaf on
of quasi coherent sheaf on
![]() with the keyword ``section wise'' and ``fiber wise'' in mind.
with the keyword ``section wise'' and ``fiber wise'' in mind.
![$\displaystyle 0\to k[X] \overset{\cdot X}{\to} k[X] \to k[X]/X k[X] \to 0.
$](img223.png)
In this example, an embedded prime