- The module
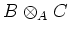
carries a natural structure of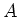 -algebra.
-algebra.
- There exits
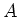 -algebra homomorphisms
-algebra homomorphisms

- The triple
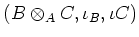 has the following universal property:
For any
has the following universal property:
For any 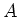 -algebra
-algebra 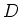 and for any
and for any 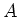 -algebra homomorphisms
-algebra homomorphisms 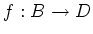 and
and 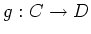 , there exists a unique
, there exists a unique 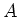 -algebra homomorphism
-algebra homomorphism
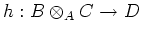
such that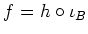 and
and
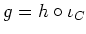 .
.