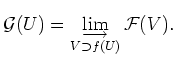
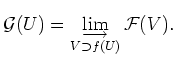
for each point
On the other hand, we have
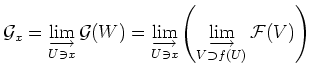
Then since the map
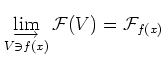
![]()
(Note that
for each point
It goes without saying that when ![]() is a (locally) ringed space,
then its open set
is a (locally) ringed space,
then its open set ![]() also carries a structure of (locally) ringed space
in a natural way, and that the inclusion map
also carries a structure of (locally) ringed space
in a natural way, and that the inclusion map ![]() is a morphism
of (locally) ringed space.
is a morphism
of (locally) ringed space.