

Next: Bibliography
Up: ``Universal representation" of Weyl
Previous: ``Universal representation" of Weyl
The answer is obtained by considering derivations.
PROOF..
(1) Since

is a derivation, we see that the set of
elements in
![$ M_p^n(k[t_1,t_2,t_3,\dots,t_{2 n}])$](img220.png)
which satisfy the
equations (
*) above form a
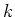
-algebra.
It is also easy that

for all

.
(2)
Any element 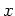 of
of
![$ M_p^n(k[t_1,t_2,t_3,\dots,t_{2 n}])$](img220.png) may be written uniquely as
may be written uniquely as
(where sum is taken over indices

)
for some polynomial

.
We may easily deduce that this happens only when

for all

.
DEFINITION 8.3
For any vector field

on

,
We define
LEMMA 8.4
 is a connection. That means,
is a connection. That means,
-
 is bi-additive
is bi-additive
- For each
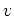 ,
,
 is a first order differential operator.
Namely, we have
is a first order differential operator.
Namely, we have
PROOF..
Easy.
LEMMA 8.5
 is the only first order differential operator on
is the only first order differential operator on
![$ M_{p^n}(k[t])$](img234.png) such that its principal symbol is
such that its principal symbol is 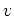 and
and
holds.
PROOF..
Let

be another first order differential operator with the same property.
Then we see that the difference
is a
![$ k[t]$](img238.png)
-linear map from
![$ M_{p^n}(k[t])$](img234.png)
to itself, and that
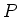
is zero
when restricted to the image

of
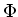
.
Since

generates
![$ M_{p^n}(k[t])$](img234.png)
as a
![$ k[t]$](img238.png)
-module, we see
immediately that
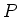
is equal to zero.
We could go further and describe fully the result obtained in the
author's papers in terms of algebras (that means, ``global'' things.)
But the author thinks it unnatural to do so without even mentioning
geometric interpretation.
So let us close the part I of this talk and proceed to a more sophisticated
world of schemes.


Next: Bibliography
Up: ``Universal representation" of Weyl
Previous: ``Universal representation" of Weyl
2007-04-20

![]() .
.
![]() of
of
![]() may be written uniquely as
may be written uniquely as


![]()

![]()