


Next: About this document ...
����� C(����) �齬���� No.12

��� 12.1
��Ĥη�
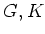
��ľ�ѤȤϡ�ľ�ѽ���
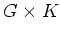
(
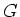
���
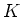
�θ��Υڥ�
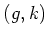
���ΤΤʤ�����)�ˡ���ˡ��
�����������ΤǤ���
���� 12.1
����ľ��
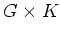
�Ͼ�ξ�ˡ�ˤ�äƷ��ˤʤ뤳�Ȥ��ʤ�����
���� 12.2 (0.5��)
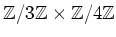
�ˤĤ��ƹͤ��Ƥߤޤ��礦��
����ϡ�����ǻ��ѷ�������ǻͳѷ����
(�����Ȥ�դ�)����ȴ�Ϣ�դ��뤳�Ȥ��Ǥ��ޤ���
| |
![$\displaystyle ([1]_3,[0]_4)\leftrightarrow$](img9.png) ������˰��ư���� ������˰��ư���� |
|
| |
![$\displaystyle ([0]_3,[1]_4)\leftrightarrow$](img10.png) ������˰��ư���� ������˰��ư���� |
|
���ơ�
![$ ([1]_3,[1]_4)$](img11.png)
�ΰ̿���
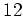
�Ǥ��뤳�Ȥ�ºݤˤ�äƤߤʤ�����
���� 12.3
����
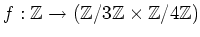
��
��������ޤ������λ���
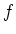 �Ͻ�Ʊ���Ǥ��뤳�Ȥ��ʤ�����
�Ͻ�Ʊ���Ǥ��뤳�Ȥ��ʤ�����
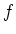 �γˤ�
�γˤ�
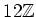 �Ǥ��뤳�Ȥ��ʤ�����
�Ǥ��뤳�Ȥ��ʤ�����
-
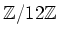 ��
��
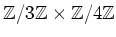 �Ȥθ��θĿ�����Ӥ��ơ�ξ�Ԥ�Ʊ���Ǥ�
�뤳�Ȥ��ʤ�����
�Ȥθ��θĿ�����Ӥ��ơ�ξ�Ԥ�Ʊ���Ǥ�
�뤳�Ȥ��ʤ�����
���� 12.4
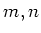
��ߤ����Ǥ����������Ȥ���Ȥ���Ʊ��
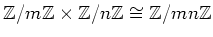
��¸�ߤ��뤳�Ȥ�
�����Ʊ�ͤ���ˡ���Ѥ��ƾ������ʤ�����
���� 12.5
������Ѥ��ơ�
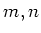
��ߤ����Ǥ����������Ȥ���Ȥ���
����
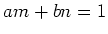
������������
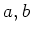
��¸�ߤ��뤳�Ȥ��ʤ�����
���� 12.6
- ����
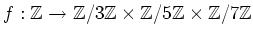 ��
��
![$ f(n)=([n]_3,[n_5],[n]_7)$](img23.png) ���������ȡ�����Ͻ�Ʊ������
�ˤʤ뤳�Ȥ��ʤ�����
���������ȡ�����Ͻ�Ʊ������
�ˤʤ뤳�Ȥ��ʤ�����
- ���
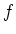 ���Ѥ��ơ�Ʊ��
���Ѥ��ơ�Ʊ��
��¸�ߤ��ʤ�����
���� 12.8
����
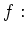
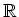
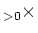
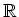
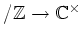
��
�ˤ������ȡ�����Ϥ��ޤ�����Ǥ��Ƥ��ơ���Ʊ���Ǥ��뤳�Ȥ��ʤ�����
����ˡ����ν�Ʊ���ϼ¤�Ʊ���Ǥ���(�Ĥޤ���ñ�ͤǤ���)���Ȥ��ʤ�
����
���� 12.9
����
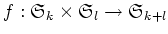
��
�ˤ���������ϡ�
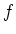
�Ͻ�Ʊ���Ǥ��뤳�Ȥ��ʤ�����
���ˡ�
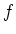
��ñ�ͤǤ��뤳�Ȥ��ʤ�����
���� 12.10
��
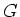
��Ϳ�����Ƥ���Ȥ��ޤ���
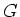
��
������ʬ��
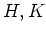
��������Ĥ��������������Ȥ���
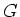
��
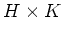
��Ʊ���Ǥ��뤳�Ȥ���
������
-
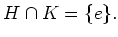
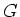 ��
�� 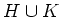 ����������롣
����������롣
����ˡ����ΤȤ�
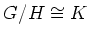
�Ǥ��뤳�Ȥ⼨���ʤ�����
���� 12.11
�ߤ����Ǥ�����
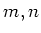
��Ϳ�����Ƥ���Ȥ��ޤ�������ˡ�
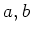
��
�������������Ȥ��ޤ������ΤȤ���Ʊ��
�εռ�����
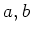
���Ѥ��Ƥ���路�ʤ�����(
![$ f^{-1}([s]_m,[t]_n)$](img48.png)
��
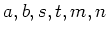
�μ��Ǥ���路�ʤ�����)
���� 12.12
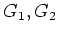
�Ϥ��줾�층����İʾ���ķ��Ȥ��ޤ������ΤȤ���
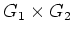
�ˤ�(�����ʤ�Τ�ޤ��)���ʤ��Ȥ�
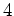
�Ĥ�������ʬ�������뤳�Ȥ��ʤ�����



Next: About this document ...
2006-07-03
![]()