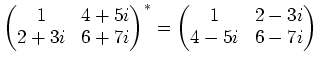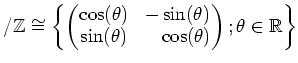Next: About this document ...
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― C(ïŋ―ïŋ―ïŋ―ïŋ―) ïŋ―é―Žïŋ―ïŋ―ïŋ―ïŋ― No.11
 ïŋ―ïŋ―ïŋ―ïŋ―ÏĄïŋ―ïŋ―ïŋ―Øīïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Éļïŋ―ĮĪïŋ―ïŋ―ïŋ―Ô·ïŋ―ïŋ―Î―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÕĪËĪÄĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ęĪ·ïŋ―ÞĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÏĄïŋ―ïŋ―ïŋ―Øīïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Éļïŋ―ĮĪïŋ―ïŋ―ïŋ―Ô·ïŋ―ïŋ―Î―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÕĪËĪÄĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ęĪ·ïŋ―ÞĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 11.3
Íïŋ―·ïŋ―
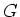
ïŋ―ïŋ―ïŋ―ïŋ―ÄĪÎļïŋ―
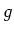
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
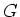
ïŋ―ïŋ―Íïŋ―Â―ïŋ―ó·ēĪïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 11.4
Ėĩïŋ―·ïŋ―
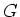
ïŋ―ïŋ―ïŋ―ïŋ―ÄĪÎļïŋ―
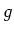
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
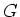
ïŋ―ïŋ―
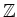
ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ïŋ―
ïŋ―ōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 11.5
-
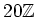 ïŋ―ïŋ―
ïŋ―ïŋ―
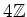 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
- ïŋ―ïŋ―ïŋ―ïŋ―
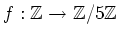 ïŋ―ïŋ―
ïŋ―ïŋ―
![$ f(x)=[x]_5$](img16.png) ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
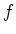 ïŋ―Ï―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪĘĪëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Ï―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪĘĪëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
- ïŋ―ïŋ―ïŋ―
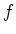 ïŋ―ÎģËĪïŋ―ïŋ―áĄĒ
ïŋ―ÎģËĪïŋ―ïŋ―áĄĒ
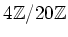 ïŋ―ïŋ―
ïŋ―ïŋ―
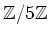 ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 11.6
ïŋ―ÏĪïŋ―ïŋ―ėĪūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―Îŧïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 11.8
ĘĢïŋ―Įŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―Ëŧïŋ―ïŋ―Äđïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―ïŋ―ïŋ―ïŋ―Îŋïŋ―Čžïŋ―ïŋ―ïŋ―ïŋ―
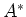
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
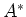
ïŋ―ÏĄïŋ―
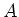
ïŋ―ïŋ―Åūïŋ―Öđïŋ―ïŋ―ïŋ―
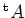
ïŋ―ÎģÆđïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽ
ïŋ―ËĪÄĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÎĪïŋ―ïŋ―ÎĪïŋ―ĘĢïŋ―Įķïŋ―ïŋ―ïŋ―ïŋ―ČĪÃĪïŋ―ïŋ―ïŋ―ÎĪĮĪïŋ―ïŋ―ïŋ―) ïŋ―ãĪĻïŋ―ÐĄïŋ―
ïŋ―Čļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îŧïŋ―ïŋ―ïŋ―
- ĘĢïŋ―Įŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―Ëŧïŋ―ïŋ―ïŋ―
 -ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― (=
-ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― (= -ïŋ―ïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―ïŋ―ÎĪïŋ―
-ïŋ―ïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―ïŋ―ÎĪïŋ―
 ïŋ―Č―ïŋ―
ïŋ―ïŋ―ïŋ―ÐĄïŋ―
ïŋ―Č―ïŋ―
ïŋ―ïŋ―ïŋ―ÐĄïŋ―
 ïŋ―Ïđïŋ―ïŋ―ïŋ―Îēïŋ―ËĄïŋ―ïŋ―
ïŋ―Ïđïŋ―ïŋ―ïŋ―Îēïŋ―ËĄïŋ―ïŋ―
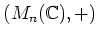 ïŋ―ïŋ―ïŋ―éĪ―ïŋ―ėžŦïŋ―ïŋ―
ïŋ―ØĪïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―éĪ―ïŋ―ėžŦïŋ―ïŋ―
ïŋ―ØĪïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
- ĘĢïŋ―Įŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―Ëŧïŋ―ïŋ―ÄēÄĩïŋ―
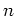 -ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― (=
-ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― (=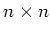 -ïŋ―ïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―ïŋ―ÎĪïŋ―
-ïŋ―ïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―ïŋ―ÎĪïŋ―
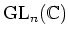 ïŋ―Č―ņĪąĪÐĄïŋ―
ïŋ―Č―ņĪąĪÐĄïŋ―
 ïŋ―ÏēÄĩÕđïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪÎĪĘĪïŋ―ïŋ―ïŋ―ËĄïŋ―ïŋ―
ïŋ―ÏēÄĩÕđïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪÎĪĘĪïŋ―ïŋ―ïŋ―ËĄïŋ―ïŋ―
 (ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČļÆĪÐĪïŋ―ïŋ―)ïŋ―ïŋ―ïŋ―éĪ―ïŋ―ėžŦïŋ―ÎĪØĪïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČļÆĪÐĪïŋ―ïŋ―)ïŋ―ïŋ―ïŋ―éĪ―ïŋ―ėžŦïŋ―ÎĪØĪïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 11.9
ĘĢïŋ―Įŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―Ëŧïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ËĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪÏĄïŋ―
(Ãąïŋ―Ėđïŋ―
ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―Äŧïŋ―ïŋ―Ëļïŋ―ïŋ―ïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―ïŋ―ïŋ―ËĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Ïūïŋ―ËĄïŋ―ËīØĪïŋ―ïŋ―Æ·ïŋ―ïŋ―ïŋ―
ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(
ïŋ―ÏĨïŋ―ËĨïŋ―ïŋ―ę·ēïŋ―ČļÆĪÐĪïŋ―ÞĪïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ― 11.10
- ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Ï―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
-
 ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
 ïŋ―ïŋ―ïŋ―ïŋ―ËĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪéĄĒ
ïŋ―ïŋ―ïŋ―ïŋ―ËĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪéĄĒ
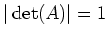 ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 11.11
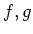
ïŋ―ÏĪČĪïŋ―Ë·ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― ïŋ―ïŋ―
ïŋ―ØĪÎ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―
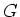
ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
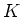
ïŋ―ïŋ―
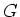
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ČĪïŋ―
ïŋ―ÂĪïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ČĪōĄĒžïŋ―ïŋ―ïŋ―ïŋ―óĪēĪÆžïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 11.12
Æąïŋ―ïŋ―
ïŋ―ïŋ―Âļïŋ―ßĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 11.13
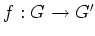
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Î―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĄïŋ―
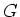
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―
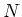
ïŋ―ïŋ―ïŋ―ïŋ―
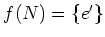
(
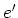
ïŋ―ïŋ―
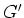
ïŋ―ïŋ―Ãąïŋ―Ėļïŋ―) ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ÐĄïŋ―
ïŋ―ïŋ―Æąïŋ―ïŋ―
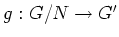
ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ÆĄïŋ―
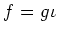
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĄïŋ―
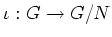
ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―Ę―ïŋ―Æąïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ČĪČĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 11.14
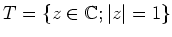
ïŋ―ïŋ―
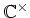
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ČĪĘĪęĄĒïŋ―ïŋ―Íūïŋ―ïŋ―
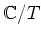
ïŋ―ïŋ―
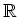
ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―



Next: About this document ...
2006-06-26
![]() ïŋ―ïŋ―ïŋ―ïŋ―ÏĄïŋ―ïŋ―ïŋ―Øīïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Éļïŋ―ĮĪïŋ―ïŋ―ïŋ―Ô·ïŋ―ïŋ―Î―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÕĪËĪÄĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ęĪ·ïŋ―ÞĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÏĄïŋ―ïŋ―ïŋ―Øīïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Éļïŋ―ĮĪïŋ―ïŋ―ïŋ―Ô·ïŋ―ïŋ―Î―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÕĪËĪÄĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ęĪ·ïŋ―ÞĪïŋ―ïŋ―ïŋ―