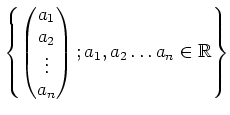

Next: About this document ...
Up: 魹ス魹ス魹ス魹ス魹ス C(魹ス魹ス魹ス魹ス) 魹ス鮨ャ魹ス魹ス魹ス魹ス No.1
Previous: 魹ス魹ス魹ス魹ス魹ス C(魹ス魹ス魹ス魹ス) 魹ス鮨ャ魹ス魹ス魹ス魹ス No.1
魹ス魹ス魹ス魹ス 1.1
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スマ。魹ス魹ス魹ステア魹スヒク魹ス魹ス魹ス魹ス魹ス
(0)魹スン、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スニ、魹ス魹スニ。魹ス
- 魹ス魹ス魹スホウン、魹ス魹ス魹ス魹スマキ魹ス魹スヒ。ツァ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス
- 魹ス魹ス魹ス魹ステア魹スフク魹ス
 魹ス魹スツク魹ス゚、魹ス魹ス魹ス
魹ス魹スツク魹ス゚、魹ス魹ス魹ス
- 魹ス魹ス魹スホセ魹ス魹ス彤サ魹ス魹スヌ、魹ス魹ス槩」
魹スネ、魹ス魹ス魹ス魹ス魹スホ、ヌ、魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スホ、ヒス魹ス魹ス魹スホク魹ス魹スユ、魹ス魹スム、魹ス魹スニスメ、ル、ハ、魹ス魹ス魹ス魹ス魹ス
(ナャ魹ス魹ス魹ス魹ス魹スワ、魹ストエ魹スル、ニ・ホ。魹ス魹ス魹ス/魹ス魹ス魹スト、ヒス㖨ュ、ハ、魹ス魹ス魹ス魹ス魹ス)
魹ス魹ス 1.1
魹ス魹ス
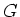
魹スホ。ヨウン、魹ス魹ス魹ス魹スラ、ネ、魹ス魹ス魹ス魹スホ、マス魹ス魹ス魹スホク魹ス魹スユ、魹スネ、魹ス魹ス魹ステア魹スヒシ魹ス魹ス魹ス
魹スホ、魹ス魹スネ、ヌ、魹ス魹ス魹ス(魹ス魹ス魹スフ、ホー魹スフ」魹スホ。ヨウン、魹ス魹ス魹ス魹スラ、ネ、マクツ、魹スハ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スユ、魹ス魹ズ、魹ス魹ス遉ヲ魹ス魹ス
魹ス魹ス魹スネ、魹ス魹ス魹ス
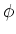
魹ス魹ス魹スツコン、ヒ、マ。魹スツュ魹ス魹ス魹ス魹ス魹スラ、ホサ魹ス魹ス筅「魹ス魹ズ、魹ス魹ス魹ス
(魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス1.2 魹ス忋イセネ、ホサ魹ス魹ス魹ス)
魹ス魹ス魹スホシ魹スホコ魹ス魹ス魹ス魹ス魹ス庹ア、槶ソ魹ス魹スヒ。魹ス
魹ス魹ス魹スホウン、魹ス魹ス魹ス魹スホサ魹ス魹ス魹スヨセ魹スヒ。魹スラ、ネ、魹ス魹ス魹ス魹スム。ラ、ネ、魹ス魹ス㖨キ、魹ス魹ス魹ス魹スユ、ヌク魹ス魹ス魹ス魹ス魹ス魹スネ、魹スツソ魹ス魹ス魹スヌ、魹ス魹ス魹ス)
魹ス魹ス魹ス魹ス 1.2
魹ス魹ス魹ズ。魹ス
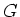
魹スネ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スホ、ホ、ハ、魹ス魹ス魹ス魹ス魹ス
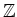
魹ス魹スネ、遙「魹ス魹スヒ。
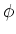
魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スミ。魹ス
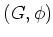
魹スマキ魹ス魹スホク魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スホ、魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹スヒ。魹ス
魹ス魹ス魹スヨ、魹ス魹ス魹ス魹スネ、魹ス魹ス魹ス
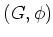
魹ス魹ス魹ス琦セ魹ス璘イ魹スヒ、ハ、槶ォ魹スノ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス(魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スハケ魹ス魹ス魹ス魹ス魹スホ、ネ、魹ス魹スヒ、魹ス魹ス魹ス魹ス魹ス魹ス魹スヘウ魹ス魹スメ、ル、魹ス魹ス魹ス魹ス魹ス魹スニ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヤ、魹ス魹スニ、゙、魹ス魹ス魹ス魹ス魹ス魹スヒク魹ス魹ス魹ス魹スホ、魹ス魹ス魹ス魹スノ、魹ス魹ス魹スハャ魹ス魹ス魹ス魹スツュ魹ス魹ス魹ス魹スニ、魹ス魹ス槶ォ魹ス魹スヘ、魹ス魹スニ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スハイ魹ス魹ス魹スニア魹スヘ。魹ス)
魹ス魹ス魹ス魹ス 1.3
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヌ。魹ス
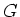
魹スネ、魹ス魹ス魹ス
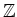
魹ス魹ス魹ス魹ス魹ス魹ス魹ス
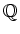
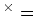
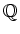
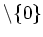
(ヘュ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スホ、魹ス魹ス魹ス 0
魹スホ、゚、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス)魹ス魹スホ、テ、魹ス魹スネ、魹ス魹スヒ、マ、ノ、魹ス魹スハ、魹ズ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 1.4
0
魹スハイ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス
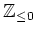
魹ス魹スツュ魹ス魹ス魹ス魹ス魹スヒ、ト、魹ス魹スニキ魹ス魹スヒ、ハ、テ、ニ、魹ス魹ズ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹スヒ、ト、魹ス魹スニ、マ、ノ、魹ス魹スヌ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 1.5
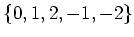
魹ス魹スツュ魹ス魹ス魹ス魹ス魹スヒエリ、魹ス魹スニキ魹ス魹スヒ、ハ、テ、ニ、魹ス魹ズ、魹ス魹ス𣇵」、ハ、魹ス魹スヌ、魹ス魹ス魹ス魹ス魹ス
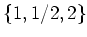
魹スマウン、魹ス魹ス魹ス魹スヒエリ、魹ス魹スニキ魹ス魹スヒ、ハ、テ、ニ、魹ス魹ズ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 1.6
ヘュ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヌ、ネ、魹ス魹ス魹ス
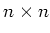
-魹ス魹ス魹ス魹ス魹ス魹ス魹スホ、ホス魹ス魹ス魹ス
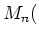
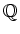
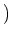
魹スヒ、ト、魹ス魹スニ。魹ス魹ス魹スヒ。魹ス魹ス魹ス魹ス魹ス魹ス魹スフセ魹スホー魹スフ」魹ス魹ス魹スム、魹ス魹ス魹ス魹ス魹ス魹ス魹ズ、魹ス魹ス魹ス魹ス魹ス魹スホス魹ス魹ス魹スマキ魹ス魹スホク魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ズ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 1.7
魹ス魹ス魹ス魹ス
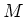
魹ス魹ス魹ス魹ス
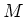
魹スリ、ホシ魹ス魹ス魹ス魹ス魹ス魹スホ、ホ、ハ、魹ス魹ス魹ス魹ス魹ス
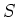
魹ス魹スヘ、魹ス魹ズ、魹ス魹ス魹ス魹ス魹ス魹スホス魹ス魹ス魹スヒセ魹スヒ。
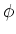
魹ス魹スヨシ魹ス魹ス魹ス魹スホケ魹ス魹ス魹ス魹ス魹スツィ魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹スヌ、魹ス魹ズ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スホ、魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
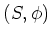
魹スマキ魹ス魹スヒ、ハ、魹ズ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 1.8
魹ス魹ス魹スホウニ。魹ス魹スホ、魹スホ、マ。魹ス魹ス魹ス魹ス魹ス魹スヒ、ハ、テ、ニ、魹ス魹ズ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヘ。魹ステア魹スヘ。魹ス魹ス魹ステア魹スヘ、ヌ、魹ス魹ス魹ス魹ス魹ス
-
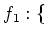 $3$ 魹ス魹ス魹スワソ魹ス
$3$ 魹ス魹ス魹スワソ魹ス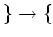 $6$ 魹ス魹ス魹スワソ魹ス
$6$ 魹ス魹ス魹スワソ魹ス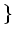 魹ス魹ス
魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スホ。魹ス
-
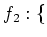 $3$ 魹ス魹ス魹スワソ魹ス
$3$ 魹ス魹ス魹スワソ魹ス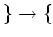 $6$ 魹ス魹ス魹スワソ魹ス
$6$ 魹ス魹ス魹スワソ魹ス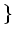 魹ス魹ス
魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スホ。魹ス
-
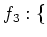 $2$ 魹ス魹ス魹スワソ魹ス
$2$ 魹ス魹ス魹スワソ魹ス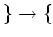 $8$ 魹ス魹ス魹スワソ魹ス
$8$ 魹ス魹ス魹スワソ魹ス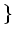 魹ス魹ス
魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スホ。魹ス
-
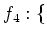 $2$ 魹ス魹ス魹スワソ魹ス
$2$ 魹ス魹ス魹スワソ魹ス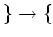 $8$ 魹ス魹ス魹スワソ魹ス
$8$ 魹ス魹ス魹スワソ魹ス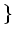 魹ス魹ス
魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スホ。魹ス
魹ス魹ス魹ス魹ス
魹ス魹ス魹スリ、ヌ、マ。魹ス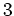 魹ス魹ス魹スワソ魹ス魹スネ、魹ス魹ス魹ス魹スミ。魹ス魹ス魹スホ、魹スホ、魹ス 0
魹ス魹ズ、゚、゙、魹ス魹ス魹ス
魹ズ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹スワソ魹ス魹スネ、魹ス魹ス魹ス魹スミ。魹ス魹ス魹スホ、魹スホ、魹ス 0
魹ス魹ズ、゚、゙、魹ス魹ス魹ス
魹ズ、魹ス魹ス魹ス魹ス魹ス
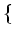 $3$ 魹ス魹ス魹スワソ魹ス
$3$ 魹ス魹ス魹スワソ魹ス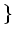 魹ス魹ス
魹スネ、魹ス魹ス魹ス魹スホ、魹ス
魹ス魹ス
魹スネ、魹ス魹ス魹ス魹スホ、魹ス 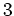 魹ス魹ス魹スワソ魹ス魹ス魹ス魹スホ、ネ、魹ス魹ス魹ス魹ス魹スフ」魹スヌ、魹ス魹ス魹ス
魹ス魹ス魹スワソ魹ス魹ス魹ス魹スホ、ネ、魹ス魹ス魹ス魹ス魹スフ」魹スヌ、魹ス魹ス魹ス
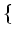
$3$ 魹ス魹ス魹スワソ魹ス
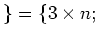
$n$ 魹ス魹ス魹ス魹ス魹ス魹ス
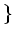
魹ス魹ス魹スホス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス
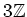 魹スネス㖨ュ、゙、魹ス魹ス魹ス
魹スネス㖨ュ、゙、魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 1.9
ハ」魹スヌソ魹ス魹ス魹ス魹スホ、ホス魹ス魹ス魹ス魹ス
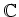
魹スネス㖨ュ、゙、魹ス魹ス魹ス
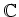
魹ス魹ス魹ス魹ス
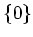
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス
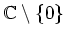
魹スマ、魹ス魹ス魹ス魹ス魹ス魹スヒエリ、魹ス魹スニキ魹ス魹ス魹スハ、魹ス魹ス魹ス魹スネ、忒ィ、魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹ステ、魹ス
魹スホオユク魹ス魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 1.10
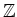
魹スヒシ魹ス魹スホ、隍ヲ魹スハア鮟サ魹ス庹、、琦ソ魹ス魹スホ、マキ魹ス魹スヌ、魹ス魹ス槶ウ魹スネ、忒ィ、魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 1.11
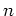
魹ス魹ス魹ス魹ス魹スツ・ル・魹ス魹スネ・魹ス魹ス魹ス魹ス
魹ス魹スツュ魹ス魹ス魹ス魹ス魹スヒエリ、魹ス魹スニキ魹ス魹スヒ、ハ、槶ォ魹スノ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス 1.1 (魹ス魹スヌァ)
魹ス魹ス
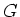
魹ス魹ス魹ス魹スハャ魹ス魹ス魹ス魹ス
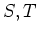
魹スヒ、ト、魹ス魹スニ。魹ス魹ス魹ス魹スホ。魹ス魹スム。魹ス
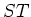
魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ズ、魹ス魹ス魹ス
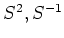
魹ス魹ス魹スヒ、ト、魹ス魹スニ、魹スニア魹スヘ、ヌ、魹ス魹ス魹ス
魹ス魹ス魹ス魹ス 1.12
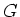
魹ス魹ス0
魹スハウ魹ス魹ス魹スヘュ魹ス魹ス魹ス魹ス魹ス魹ス魹スホ、ヒセ魹スヒ。魹ス魹ス魹スフセ魹スホウン、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スネ、魹ス魹ズ、魹ス魹ス魹ス
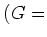
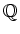
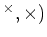
魹ス魹ス魹ス魹ス魹スホサ魹ス魹ス魹ス
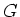
魹ス魹ス魹ス魹スハャ魹ス魹ス魹ス魹ス
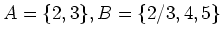
魹スヒ、ト、魹ス魹スニ。魹ス
魹ス魹スラサ魹ス魹ス魹ス魹スハ、魹ス魹ス魹ス魹ス魹ス
(魹ス魹ス)
http://www.math.kochi-u.ac.jp/docky/kogi/
魹スヒ・魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スネ。魹ス魹ス魹ス魹スホ・ラ・魹ス魹スネシ魹ス魹スホ、魹ス魹スネ、魹ズ、魹ス魹スホ、ヌ。魹ス
魹ス魹ス魹ス魹ス魹スホサ魹ス魹スヨ、ヒ、ネ、魹スツサ魹スハ、テ、魹ス魹スヘ、マ。魹ス魹スニシ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スネ、テ、ニ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス


Next: About this document ...
Up: 魹ス魹ス魹ス魹ス魹ス C(魹ス魹ス魹ス魹ス) 魹ス鮨ャ魹ス魹ス魹ス魹ス No.1
Previous: 魹ス魹ス魹ス魹ス魹ス C(魹ス魹ス魹ス魹ス) 魹ス鮨ャ魹ス魹ス魹ス魹ス No.1
2006-04-11
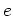 魹ス魹スツク魹ス゚、魹ス魹ス魹ス
魹ス魹スツク魹ス゚、魹ス魹ス魹ス