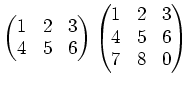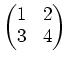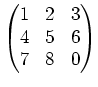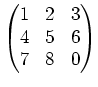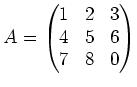: ïŋ―ïŋ―ïŋ―ïŋ―Ęļïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―...
ïŋ―ïŋ―ïŋ―ïŋ―Øąé―Ž I ïŋ―ïŋ―ïŋ―ïŋ― No.5

ïŋ―ïŋ―ïŋ―ïŋ― 5.3
-
 ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
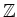 ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
-
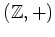 ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ōĪđĪŲĪÆĩïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ōĪđĪŲĪÆĩïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
-
![$ ({\mathbb{C}}[X],+)$](img18.png) ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ĮĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ĮĄïŋ―
![$ {\mathbb{C}}[X]$](img11.png) ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĮĪÏĪĘĪïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―óĪēĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĮĪÏĪĘĪïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―óĪēĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 5.4
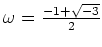
(
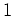
ïŋ―Îŧïŋ―ïŋ―蚎)ïŋ―ČĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îŧïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―
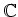
ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ÄĪĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ËĄïŋ―ËīØĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―) ïŋ―ïŋ―ïŋ―ÎīÄĪÏĄïŋ―
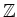
ïŋ―ËĄïŋ―
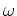
ïŋ―ïŋ―ïŋ―ÕĪïŋ―ïŋ―ÃĪïŋ―ïŋ―ïŋ―ïŋ―ÄĪËĪĘĪÃĪÆĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĄïŋ―ïŋ―ïŋ―ïŋ―ÎīÄĪÎĪïŋ―ïŋ―ČĪïŋ―
![$ {\mbox{${\mathbb{Z}}$}}[\omega]$](img24.png)
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 5.5
-
![$ {\mbox{${\mathbb{Z}}$}}[\omega]$](img24.png) (ïŋ―ïŋ―ïŋ―äŧēïŋ―ïŋ―) ïŋ―ïŋ―Ãąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ïŋ―äŧēïŋ―ïŋ―) ïŋ―ïŋ―Ãąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
-
![% latex2html id marker 1160
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{3}]={\mbox{${\mathbb{Z}}$}}+{\mbox{${\mathbb{Z}}$}}\sqrt{3}$](img25.png) ïŋ―ïŋ―Ãąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Ãąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ― 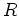 ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―ïŋ―ïŋ―ïŋ―Îļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ËĪïŋ―Äđïŋ―ïŋ―ïŋ―ïŋ―ÍĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―
ïŋ―Ėūïŋ―ΰïŋ―ĖĢïŋ―ïŋ―ïŋ―ÂĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ČĪïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―ïŋ―ïŋ―ĮŊïŋ―ïŋ―ïŋ―Į―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪÞĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―ïŋ―ïŋ―ïŋ―Îļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ËĪïŋ―Äđïŋ―ïŋ―ïŋ―ïŋ―ÍĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―
ïŋ―Ėūïŋ―ΰïŋ―ĖĢïŋ―ïŋ―ïŋ―ÂĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ČĪïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―ïŋ―ïŋ―ĮŊïŋ―ïŋ―ïŋ―Į―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪÞĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
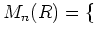
$R$ ïŋ―Îļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ËĪïŋ―ïŋ― $n×#times;n$ ïŋ―ïŋ―ïŋ―ïŋ―
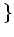
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―Äīïŋ―ïŋ―ĮĪÏĪĘĪïŋ―)ïŋ―ÄĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―Ãąïŋ―Ėļïŋ―ïŋ―ïŋ― 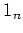 (
(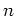 ïŋ―ïŋ―ïŋ―ïŋ―Ãąïŋ―Ėđïŋ―ïŋ―ïŋ―).
ïŋ―ïŋ―ïŋ―ïŋ―Ãąïŋ―Ėđïŋ―ïŋ―ïŋ―).
ïŋ―ïŋ―ïŋ―ïŋ― 5.7
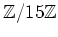
ïŋ―Îļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ËĪïŋ―Äđïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ãąïŋ―Ę·ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÍĪïŋ―
14ïŋ―Ęēïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ÃĪïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪĘĪïŋ―čĪĶïŋ―ïŋ―Äūïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 5.8
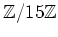
ïŋ―Îļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪËĪïŋ―Äđïŋ―ïŋ―ïŋ―
ïŋ―ÎĩÕđïŋ―ïŋ―ïŋ―ïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 5.9
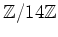
ïŋ―Îļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪËĪïŋ―Äđïŋ―ïŋ―ïŋ―
ïŋ―ÎĩÕđïŋ―ïŋ―ïŋ―ïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 5.10
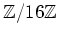
ïŋ―Îļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪËĪïŋ―Äđïŋ―ïŋ―ïŋ―
ïŋ―ÎĩÕđïŋ―ïŋ―ïŋ―ïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ïŋ―ïŋ―ΰĘēïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪÏđïŋ―ïŋ―óž°Īïŋ―ČĨėĄžïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Íģïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ― 5.11
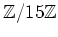
ïŋ―Îļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪËĪïŋ―Äđïŋ―ïŋ―ïŋ―
ïŋ―ÎĩÕđïŋ―ïŋ―ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Íģïŋ―ïŋ―óĪēĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ŌĨïŋ―ïŋ―:
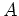
ïŋ―ÎĩÕđïŋ―ïŋ―ïŋ―
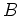
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
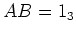
(3ïŋ―ïŋ―ïŋ―ïŋ―Ãąïŋ―Ėđïŋ―ïŋ―ïŋ―).
Îūïŋ―ÕĪïŋ― ïŋ―ïŋ―ïŋ―óž°Īïŋ―ČĪïŋ―ïŋ―...)
ïŋ―ïŋ―ïŋ―ïŋ― 5.12
ïŋ―ÉĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
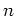
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪâĄĒ
ïŋ―ïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
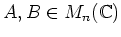
ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ŌĨïŋ―ïŋ―:ïŋ―ČĨėĄžïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ― 5.13
ïŋ―Įŋïŋ―
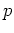
ïŋ―ËĪÄĪïŋ―ïŋ―ÆĄïŋ―
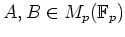
ïŋ―ĮĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―óĪēĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
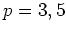
ïŋ―ÎĪČĪïŋ―ïŋ―ËĪÞĪïŋ―ïŋ―îĪ·ïŋ―ÆĪßĪïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ĘĪïŋ―ïŋ―ïŋ―)



: ïŋ―ïŋ―ïŋ―ïŋ―Ęļïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―...
Ęŋïŋ―ïŋ―17ĮŊ11ïŋ―ïŋ―4ïŋ―ïŋ―
![]()
![]() ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―ïŋ―ïŋ―ïŋ―Îļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ËĪïŋ―Äđïŋ―ïŋ―ïŋ―ïŋ―ÍĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―
ïŋ―Ėūïŋ―ΰïŋ―ĖĢïŋ―ïŋ―ïŋ―ÂĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ČĪïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―ïŋ―ïŋ―ĮŊïŋ―ïŋ―ïŋ―Į―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪÞĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―ïŋ―ïŋ―ïŋ―Îļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ËĪïŋ―Äđïŋ―ïŋ―ïŋ―ïŋ―ÍĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―
ïŋ―Ėūïŋ―ΰïŋ―ĖĢïŋ―ïŋ―ïŋ―ÂĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ČĪïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―ïŋ―ïŋ―ĮŊïŋ―ïŋ―ïŋ―Į―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪÞĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―