


: ����ʸ��ˤĤ���...
documentclass[12pt]amsart
usepackageeucal,amssymb
par
newedtheoremtheorem����[section]newedtheoremnitheorem���ޤ���פǤʤ�����[section]renewedcommandthenitheorem
newedtheoremrefpropPropositionrenewedcommandtherefprop
newedtheoremcorollary��[section]newedtheoremlemma����[section]newedtheoremfact����[section]newedtheoremproposition[theorem]̿��newedtheoremaxAxiompar
theoremstyledefinition
newedtheoremdfn���[section] newedtheoremexmp��[section] newedtheoremexample��[section]newedtheoremdefinition���[section] newedtheoremq����[section] newedtheoremexq����[section] newedtheoremkeywd���ؤΥ������par
theoremstyleremark
newedtheoremrem����[section]newedtheoremclaim[]renewedcommandtheclaim par
numberwithinequationsection
par
newedcommandtheoremref[1]Theorem ref#1
newedcommandsecref[1]Sref#1
newedcommandlemref[1]Lemma ref#1
par
newedcommandZmbox
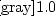 newedcommandQmbox
newedcommandQmbox
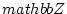 newedcommandRmbox
newedcommandRmbox
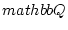 newedcommandNmbox
newedcommandNmbox
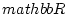 newedcommandImbox
newedcommandImbox
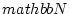 par
newedcommandLeg[2]mbox
par
newedcommandLeg[2]mbox
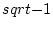 newedcommandFpmbox
newedcommandFpmbox
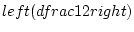 newedcommandkpekembox
newedcommandkpekembox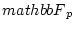 newedcommandbigzerolsmashhboxhuge 0
newedcommandbigzerousmashlower1.7exhboxhuge 0
par
begindocument
title[�����II ���� No.thistime ]�����II ���� No.thistime
par
quad
vskip -3pc
maketitle
par
setcountersectionthistime
par
�����Υơ���
par
fbox��ʬ������;������;���硢�饰��������
par
���������Ϥäơ������ΰ�̣�⤳��Ʒ����ν���ɤäƤߤ褦��
â�����Ϥ��ʤ��ᤤ�����C�� ���I ���ʳ��Ǥϰ���ʤ��ä�
�����Τ�ʤ�ʣ������ⰷ����礬���뤫�顢���դ��뤳�ȡ�
par
�ޤ����轵�ֵ��ǤϿ��줿������ˤϽʤ��ä��Τǡ����������
�Ƥ�����
begintheorem_type[definition][definition][section][definition][][]
newedcommandbigzerolsmashhboxhuge 0
newedcommandbigzerousmashlower1.7exhboxhuge 0
par
begindocument
title[�����II ���� No.thistime ]�����II ���� No.thistime
par
quad
vskip -3pc
maketitle
par
setcountersectionthistime
par
�����Υơ���
par
fbox��ʬ������;������;���硢�饰��������
par
���������Ϥäơ������ΰ�̣�⤳��Ʒ����ν���ɤäƤߤ褦��
â�����Ϥ��ʤ��ᤤ�����C�� ���I ���ʳ��Ǥϰ���ʤ��ä�
�����Τ�ʤ�ʣ������ⰷ����礬���뤫�顢���դ��뤳�ȡ�
par
�ޤ����轵�ֵ��ǤϿ��줿������ˤϽʤ��ä��Τǡ����������
�Ƥ�����
begintheorem_type[definition][definition][section][definition][][]
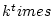 �����Ǥ���Ȥϡ�
beginenumerate
setcounterenumi-1
renewedcommandlabelenumi(��arabicenumi)
item �黻
�����Ǥ���Ȥϡ�
beginenumerate
setcounterenumi-1
renewedcommandlabelenumi(��arabicenumi)
item �黻
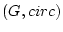 �ϼ����Ǥ��롣�Ĥޤꡢ
�ϼ����Ǥ��롣�Ĥޤꡢ
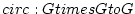 �θ���Ĥ���
�θ���Ĥ��� 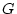 ���Ф���
���Ф��� 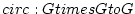 �θ�
�θ�
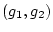 ��
��ޤ롣
item
��
��ޤ롣
item 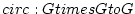 �α黻
�α黻 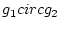 �Ϸ��Χ��ߤ�����
item
�Ϸ��Χ��ߤ�����
item 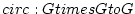 �ˤ�ñ�̸���¸�ߤ��롣
item
�ˤ�ñ�̸���¸�ߤ��롣
item 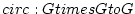 �γƸ��ˤϵո���¸�ߤ��롣
endenumerate
�ξ�郎���������Ȥ��ˤ�����endtheorem_type
(�黻
�γƸ��ˤϵո���¸�ߤ��롣
endenumerate
�ξ�郎���������Ȥ��ˤ�����endtheorem_type
(�黻 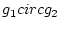 �����Ǥ��뤫�ä�ή�줫��λ��ѤߤΤȤ��ˤϡ�
�����Ǥ��뤫�ä�ή�줫��λ��ѤߤΤȤ��ˤϡ�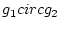 ��
����ñ��
��
����ñ�� 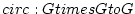 �Τ��ȤȸƤ֤��Ȥ�¿����)
��
�Τ��ȤȸƤ֤��Ȥ�¿����)
�� 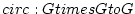 �θ��θĿ��Τ��Ȥΰ̿��ȸƤӡ�
�θ��θĿ��Τ��Ȥΰ̿��ȸƤӡ�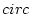 �ǽ�ɽ����
par
����Ϳ������ȡ�������ʬ�����ɤΤ褦�ʤ�Τ���ͤ���Τ�
����Ū�Ǥ��롣��ʬ��������ϴ�ñ�ǡ�
par
begintheorem_type[definition][definition][section][definition][][]
��
�ǽ�ɽ����
par
����Ϳ������ȡ�������ʬ�����ɤΤ褦�ʤ�Τ���ͤ���Τ�
����Ū�Ǥ��롣��ʬ��������ϴ�ñ�ǡ�
par
begintheorem_type[definition][definition][section][definition][][]
�� 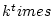 ����ʬ���Ȥϡ�
����ʬ���Ȥϡ�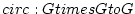 ����ʬ����
����ʬ���� 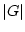 �Ǥ��äơ�
�Ǥ��äơ�
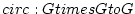 �α黻
�α黻 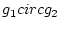 �����¤��뤳�Ȥˤ��
�����¤��뤳�Ȥˤ�� 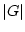 ���Ȥ����ˤʤäƤ���
�Ȥ��ˤ�����endtheorem_type
par
���ơ���
���Ȥ����ˤʤäƤ���
�Ȥ��ˤ�����endtheorem_type
par
���ơ��� 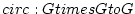 �Ȥ�����ʬ��
�Ȥ�����ʬ�� 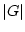 ����ޤä��Ȥ�����;����
����ޤä��Ȥ�����;���� 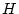 ��
�������롣�����
��
�������롣����� 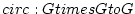 �Ρ֥��饹ʬ���פˤ�ä���ޤ롣
par
begintheorem_type[definition][definition][section][definition][][]
�Ρ֥��饹ʬ���פˤ�ä���ޤ롣
par
begintheorem_type[definition][definition][section][definition][][]
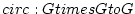 ����ʬ��
����ʬ�� 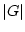 ��Ϳ�����Ƥ���Ȥ���
��Ϳ�����Ƥ���Ȥ���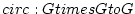 �Υ��饹ʬ�������Τ褦����ޤ롣
vskip baselineskip
noindent
�Υ��饹ʬ�������Τ褦����ޤ롣
vskip baselineskip
noindent
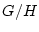 ��
�� 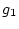 ��Ʊ�����饹
��Ʊ�����饹 
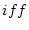 �Ȥʤ�
�Ȥʤ� 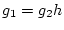 ��¸�ߤ��롣
vskip baselineskip
beginenumerate
item ���Υ��饹ʬ���ˤ��
��¸�ߤ��롣
vskip baselineskip
beginenumerate
item ���Υ��饹ʬ���ˤ�� 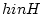 �Υ��饹��
�Υ��饹�� 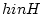 ��
�� 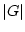 �˴ؤ��뺸��;��ȸƤ֡�
item ���Υ��饹ʬ���ˤ�륯�饹�����Τν����
�˴ؤ��뺸��;��ȸƤ֡�
item ���Υ��饹ʬ���ˤ�륯�饹�����Τν���� 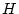 �Ƚ�
�Ƚ�
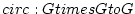 ��
�� 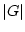 �ˤ�뺸��;����ȸƤ�
endenumerate
parendtheorem_type
newpage
par
begintheorem_type[theorem][theorem][section][][][]
beginenumerate
item
�ˤ�뺸��;����ȸƤ�
endenumerate
parendtheorem_type
newpage
par
begintheorem_type[theorem][theorem][section][][][]
beginenumerate
item 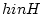 ��
�� 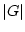 �ˤ�뺸��;������Τ�
����������
item
�ˤ�뺸��;������Τ�
����������
item 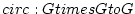 ��ͭ�·��ΤȤ���
(���
��ͭ�·��ΤȤ���
(â����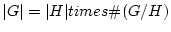 �Ͻ���
�Ͻ��� 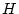 �θ��θĿ�)
item �Ȥ��ˡ�
�θ��θĿ�)
item �Ȥ��ˡ�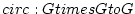 ��ͭ�·��ʤ�С�
��ͭ�·��ʤ�С�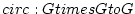 ����ʬ��
����ʬ�� 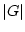 �ΰ̿�(���θĿ�)
�ΰ̿�(���θĿ�) 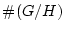 ��
���ʤ餺
��
���ʤ餺 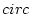 ������Ǥ��롣(�饰��������)
endenumerate
parendtheorem_type
�饰��������(�ȡ������ü�ʾ��Ȥ��Ƽ���˰����ե���ޡ��ξ�����)�ϡ�
�̿������ˤȤäƽ��פǤ��뤳�Ȥ᤹�ǽ����Ǥ�������
par
begintheorem_type[q][q][section][definition][][]
��
������Ǥ��롣(�饰��������)
endenumerate
parendtheorem_type
�饰��������(�ȡ������ü�ʾ��Ȥ��Ƽ���˰����ե���ޡ��ξ�����)�ϡ�
�̿������ˤȤäƽ��פǤ��뤳�Ȥ᤹�ǽ����Ǥ�������
par
begintheorem_type[q][q][section][definition][][]
��
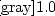 �θ�
�θ� 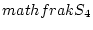 ��
��
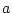 ����ᡢ
�Ȥ��������ΤȤ�
����ᡢ
�Ȥ��������ΤȤ� 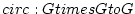 ��
�� 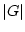 �ˤ�륯�饹ʬ����ɽ��ºݤ˽ʤ�����endtheorem_type
par
begintheorem_type[q][q][section][definition][][]
��
�ˤ�륯�饹ʬ����ɽ��ºݤ˽ʤ�����endtheorem_type
par
begintheorem_type[q][q][section][definition][][]
��
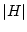 ����ʬ��
����ʬ�� 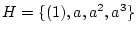 �ǡ��̿���
�ǡ��̿��� 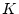 �ʾ�
�ʾ� 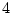 �ʲ��Τ��
����
(������
�ʲ��Τ��
����
(������ 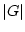 ����������)
���ĸ��Ĥ�����������
����������)
���ĸ��Ĥ����������� 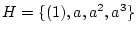 ���Ф���
������ 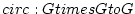 ��
�� 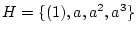 �ˤ��
���饹ʬ����ɽ��ºݤ˽ʤ�����endtheorem_type
par
enddocument
�ˤ��
���饹ʬ����ɽ��ºݤ˽ʤ�����endtheorem_type
par
enddocument
ʿ��16ǯ7��12��