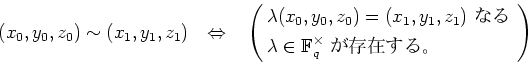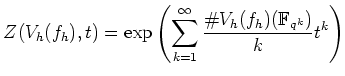�����Υơ���
![]()
![]() �˴ؤ���
�˴ؤ���
![]() �����
����� ![]() ��뤳�Ȥˤ�ꡢ
��뤳�Ȥˤ�ꡢ
![]() ���������
��������� ![]() �������ޤ롣
���Ĥ�����ˤĤ��Ƥ��ι�Ʊ�������ؿ�����褦��
�������ޤ롣
���Ĥ�����ˤĤ��Ƥ��ι�Ʊ�������ؿ�����褦��
I. ��ʪ��
![]()
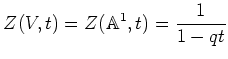
II. ���
![]()
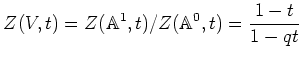
III. (��)��
![]()

3�Ĥˤ϶��������ʤ����������� �¤�ʿ�̤ˡ�̵�±����פ��դ��ä���Ȥ���餬����Ū��į�����褦�ˤʤ롣
���̤ˡ�![]() ����
���� ![]() ���Ф��ơ�
���Ф��ơ�
![]() ��
�� ![]() ��
�Ƽ����ȸƤ֡�����
��
�Ƽ����ȸƤ֡�����
![]() �ˡ����Τ褦�ʥ��饹ʬ����Ƴ�����롣
�ˡ����Τ褦�ʥ��饹ʬ����Ƴ�����롣