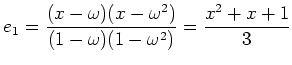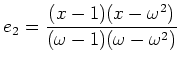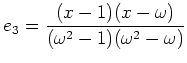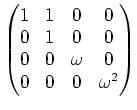: пњљпњљпњљпњљ ЄпњљпњљЋ§ƒ§пњљпњљпњљ...
пњљпњљпњљпњљпњљII пњљоЄ≥ќђпњљпњљ
пњљпњљпњљпњљ 14.1
пњљпњљпњљќ•пњљу•∞њёЈпњљ
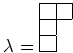
пњљЋ§ƒ§пњљпњљ∆°пњљ
![$ {\mathbb{C}}[\mathfrak{S}_4]$](img3.png)
пњљќЄпњљ
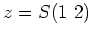
пњљпњљ…љпњљпњљ
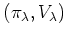
пњљпњљ
пњљ…§ќ§и§¶пњљ Їпњљпњљ—§пњљ‘§пњљпњљпњљпњљпњљпњљ“§пњљпњљ §пњљпњљпњљпњљпњљ
(ќђпњљпњљ)
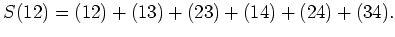 |
(пњљпњљ) |
пњљпњљпњљпњљпњљ
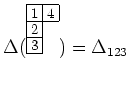 пњљЋЇпњљпњљ—§пњљпњљпњљпњљл§≥пњљ»§пњљ
пњљЌ§пњљпњљпњљ–§и§§пњљпњљ
(пњљпњљ)пњљќ±пњљпњљ’§ќЇ«љпњљпњљ3пњљпњљпњљ
пњљЋЇпњљпњљ—§пњљпњљпњљпњљл§≥пњљ»§пњљ
пњљЌ§пњљпњљпњљ–§и§§пњљпњљ
(пњљпњљ)пњљќ±пњљпњљ’§ќЇ«љпњљпњљ3пњљпњљпњљ
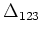 пњљпњљ
пњљпњљ 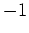 пњљ№§«Їпњљпњљ—§пњљпњљл°£
пњљпњљпњљ»§пњљ3пњља§ђпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљ№§«Їпњљпњљ—§пњљпњљл°£
пњљпњљпњљ»§пњљ3пњља§ђпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљ»§пњљ√§∆°пњљ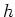 пњљпњљ„їпњљпњљпњљпњљпњљ–§и§§пњљп§±пњљпњљпњљпњљпњљпњљƒЊпњљЋЈ„їпњљпњљпњљпњљ∆§пњљи§§пњљпњљпњљпњљпњљпњљпњљќ§и§¶пњљпњљ
пњљЌ§пњљпњљпњљ»≥Џ§Ћ§ §л°£
ћњпњљпњљ9.1пњљЋ§пњљк°Ґ
пњљпњљ„їпњљпњљпњљпњљпњљ–§и§§пњљп§±пњљпњљпњљпњљпњљпњљƒЊпњљЋЈ„їпњљпњљпњљпњљ∆§пњљи§§пњљпњљпњљпњљпњљпњљпњљќ§и§¶пњљпњљ
пњљЌ§пњљпњљпњљ»≥Џ§Ћ§ §л°£
ћњпњљпњљ9.1пњљЋ§пњљк°Ґ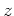 пњљќЇпњљпњљ—§пњљпњљпњљпњљпњљ№§«§пњљпњљпњљѕ§пњљпњљ«§пњљпњљл§≥пњљ»§пњљ ђпњљпњљпњљ√§∆§пњљпњљпњљќ§«°пњљ
пњљќЇпњљпњљ—§пњљпњљпњљпњљпњљ№§«§пњљпњљпњљѕ§пњљпњљ«§пњљпњљл§≥пњљ»§пњљ ђпњљпњљпњљ√§∆§пњљпњљпњљќ§«°пњљ
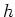 пњљпњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљпњљ
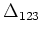 пњљпњљпњљ№њпњљпњљ«§ §пњљпњљпњљ–§ §пњљ §пњљпњљп§±пњљ«§пњљпњљл°£
пњљпњљпњљ §пњљпњљпњљпњљ≈Єпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљ№њпњљпњљ«§ §пњљпњљпњљ–§ §пњљ §пњљпњљп§±пњљ«§пњљпњљл°£
пњљпњљпњљ §пњљпњљпњљпњљ≈Єпњљпњљпњљпњљпњљпњљпњљ 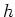 пњљпњљ
пњљпњљ 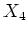 пњљпњљё§ё§ §пњљпњљпњљпњљЋ§ §л°£пњљпњљпњљпњљпњљпњљпњљ√§∆°пњљ
пњљ»§ §√§∆§пњљпњљпњљѕ§пњљпњљ«§пњљпњљк°Ґпњљпњљпњљ’§ѕ§пњљпњљпњљпњљпњљ
пњљпњљё§ё§ §пњљпњљпњљпњљЋ§ §л°£пњљпњљпњљпњљпњљпњљпњљ√§∆°пњљ
пњљ»§ §√§∆§пњљпњљпњљѕ§пњљпњљ«§пњљпњљк°Ґпњљпњљпњљ’§ѕ§пњљпњљпњљпњљпњљ
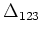 пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ»§пњљ
пњљќ§пњљпњљпњљпњљпњљл°£
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ»§пњљ
пњљќ§пњљпњљпњљпњљпњљл°£
пњљё§»§пњљпњљ»°пњљ
пњљпњљпњљ §пњљпњљ 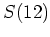 пњљпњљ
пњљпњљ 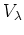 пњљпњљ
пњљпњљ 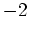 пњљ№§»§пњљпњљ∆Їпњљпњљ—§пњљпњљл°£
(ћњпњљпњљ9.1 пњљЋ§пњљк°Ґ
пњљ№§»§пњљпњљ∆Їпњљпњљ—§пњљпњљл°£
(ћњпњљпњљ9.1 пњљЋ§пњљк°Ґ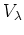 пњљпњљ
пњљпњљ 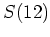 пњљѕ•пњљпњљпњљпњљй°Љпњљ»§пњљпњљ∆Їпњљпњљ—§пњљпњљл§Ђпњљй°Ґ
пњљпњљќ§и§¶пњљпњљ
пњљѕ•пњљпњљпњљпњљй°Љпњљ»§пњљпњљ∆Їпњљпњљ—§пњљпњљл§Ђпњљй°Ґ
пњљпњљќ§и§¶пњљпњљ
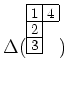 пњљЎ§ќЇпњљпњљ—§пњљЌ§пњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљ ђпњљ«§пњљпњљпњљќ§пњљпњљпњљпњљпњљ«Љпњљпњљпњљпњљпњљпњљпњљпњљпњљ §пњљпњљЌ§пњљ
пњљЎ§ќЇпњљпњљ—§пњљЌ§пњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљ ђпњљ«§пњљпњљпњљќ§пњљпњљпњљпњљпњљ«Љпњљпњљпњљпњљпњљпњљпњљпњљпњљ §пњљпњљЌ§пњљ
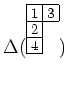 пњљпњљпњљќЊпњљќЇпњљпњљ—§пњљ∆§пњљпњљпњљ∆§я§∆§пњљи§§пњљпњљ
Єпњљпњљпњљпњљпњљ’§пњљпњљЎ§пњљпњљпњљпњљпњљпњљпњљ∆±пњљпњљпњљпњљпњљ»§т§Ј§∆§пњљпњљпњљќ§пњљпњљпњљпњљпњљ«§пњљпњљпњљ»ї„§пњљпњљпњљ)
пњљпњљпњљќЊпњљќЇпњљпњљ—§пњљ∆§пњљпњљпњљ∆§я§∆§пњљи§§пњљпњљ
Єпњљпњљпњљпњљпњљ’§пњљпњљЎ§пњљпњљпњљпњљпњљпњљпњљ∆±пњљпњљпњљпњљпњљ»§т§Ј§∆§пњљпњљпњљќ§пњљпњљпњљпњљпњљ«§пњљпњљпњљ»ї„§пњљпњљпњљ)
пњљпњљпњљпњљ 14.2
![$ {\mathbb{C}}[\mathfrak{S}_4]$](img3.png)
пњљќЄпњљ
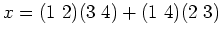
пњљ»°пњљ
4пњљпњљпњљќ•пњљу•∞њёЈпњљ
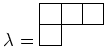
пњљпњљпњљ–§пњљпњљ∆°пњљ
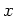
пњљпњљ
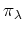
пњљпњљпњљ…љпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
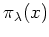
пњљпњљ
пњљ«Њпњљ¬њпњљаЉ∞пњљпњљпњљпњљ §пњљпњљпњљпњљпњљ
(ќђпњљпњљ)
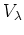 пњљѕЉпњљпњљќ§и§¶пњљпњљЌњпњљпњљпњљпњљпњљл°£
пњљѕЉпњљпњљќ§и§¶пњљпњљЌњпњљпњљпњљпњљпњљл°£
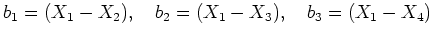 пњљ»§пњљпњљпњљпњљ»°пњљ
пњљ»§пњљпњљпњљпњљ»°пњљ
пњљпњљпњљ §пњљпњљпњљпњљ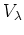 пњљќіпњљпњљпњљ»§пњљпњљпњљ
пњљќіпњљпњљпњљ»§пњљпњљпњљ
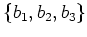 пњљпњљпњљпњљ—§пњљпњљпњљпњљ»§пњљпњљпњљ
пњљпњљпњљпњљ—§пњљпњљпњљпњљ»§пњљпњљпњљ
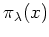 пњљпњљ…љпњљпњљпњљпњљпњљпњљѕ°пњљ
пњљпњљЌњпњљпњљпњљпњљпњљл°£
пњљпњљпњљќєпњљпњљпњљпњљпњљпњљпњљпњљ¬њпњљаЉ∞пњљпњљ
пњљпњљ…љпњљпњљпњљпњљпњљпњљѕ°пњљ
пњљпњљЌњпњљпњљпњљпњљпњљл°£
пњљпњљпњљќєпњљпњљпњљпњљпњљпњљпњљпњљ¬њпњљаЉ∞пњљпњљ
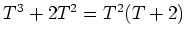 . пњљ„їпњљпњљпњљпњљ∆§я§пњљпњљ ђпњљпњљпњљл§ђпњљпњљ
пњљ«Њпњљ¬њпњљаЉ∞пњљпњљ
. пњљ„їпњљпњљпњљпњљ∆§я§пњљпњљ ђпњљпњљпњљл§ђпњљпњљ
пњљ«Њпњљ¬њпњљаЉ∞пњљпњљ 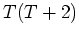 пњљ«§пњљпњљл°£
(пњљпњљпњљпњљпњљ
пњљ«§пњљпњљл°£
(пњљпњљпњљпњљпњљ 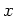 пњљпњљ
пњљпњљ
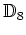 пњљќЈпњљпњљƒ§пњљпњљжњіпњљпњљпњљ»§пњљя§л§≥пњљ»§пњљпњљ«§пњљпњљпњљ
пњљпњљпњљпњљпњљя§ §пњљпњљпњљпњљпњљпњљпњљ10.1пњљпњљпњљ—§пњљпњљл§≥пњљ»§пњљ«§пњљпњљл°£)
пњљќЈпњљпњљƒ§пњљпњљжњіпњљпњљпњљ»§пњљя§л§≥пњљ»§пњљпњљ«§пњљпњљпњљ
пњљпњљпњљпњљпњљя§ §пњљпњљпњљпњљпњљпњљпњљ10.1пњљпњљпњљ—§пњљпњљл§≥пњљ»§пњљ«§пњљпњљл°£)
пњљпњљпњљпњљ 14.3
£пњљ«њпњљпњљпњљ
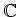
пњљпњљпњљпњљ ђпњљƒ§»§пњљпњљ∆іё§пњљпњљ
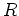
пњљќЄпњљ
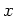
пњљќЇ«Њпњљ¬њпњљаЉ∞пњљпњљ
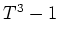
пњљ«§пњљпњљпњљ»§пњљпњљпњљпњљпњљпњљќ§и§¶пњљ Њпњљпњљпњљ∆±пњљпњљпњљпњљпњљпњљ¬≠пњљпњљпњљпњљ
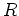
пњљќЄпњљ
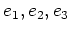
пњљпњљ
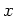
пњљпњљпњљ—§пњљпњљ∆Їпњљпњљ §пњљпњљпњљпњљпњљ
-
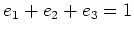
-
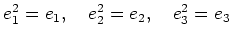
-
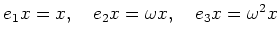
пњљпњљпњљпњљпњљпњљпњљпњљ
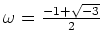
(
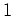
пњљпњљ3пњљиЇђпњљќ∞пњљпњљ)пњљ»§пњљпњљл°£
(ќђпњљпњљ)
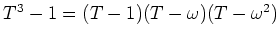 пњљ«§пњљпњљк°Ґ
пњљ«§пњљпњљк°Ґ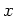 пњљт§љ§ќЄпњљЌ≠пњљЌ§Ћ§пњљ√§пњљ
ђпњљт§Ј§и§¶пњљ»§пњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
пњљт§љ§ќЄпњљЌ≠пњљЌ§Ћ§пњљ√§пњљ
ђпњљт§Ј§и§¶пњљ»§пњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
пњљ»§пњљпњљ–§и§§пњљпњљ
пњљпњљпњљпњљ 14.4
пњљпњљпњљќ§и§¶пњљ Њпњљпњљпњљ∆±пњљпњљпњљпњљпњљпњљ¬≠пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
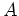
пњљпњљпњљпњљпњљу§≤§и°£(пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ §пњљ)
пњљпњљпњљпњљпњљпњљпњљпњљ
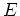
пњљпњљ(
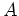
пњљпњљ∆±пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ)√±пњљћєпњљпњљпњљ«§пњљпњљл°£
-
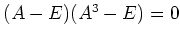
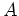 пњљпњљпњљпњљпњљпњљпњљпњљ3пњљпњљпњљќіЎЈпњљпњљпњљпњљпњљпњљпњљ¬≠пњљпњљпњљ §пњљпњљпњљ
пњљпњљпњљпњљпњљпњљпњљпњљ3пњљпњљпњљќіЎЈпњљпњљпњљпњљпњљпњљпњљ¬≠пњљпњљпњљ §пњљпњљпњљ
(ќђпњљпњљ)
㧮–Љпњљпњљќ§и§¶пњљ §пњљќ§пњљпњљпњљпњљл°£
пњљпњљпњљпњљпњљпњљ 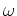 пњљпњљ пњљпњљпњљпњљпњљ∆±пњљпњљпњљпњљ
пњљпњљ пњљпњљпњљпњљпњљ∆±пњљпњљпњљпњљ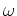 пњљќ§и§¶пњљпњљ £пњљ«њпњљпњљпњљпњљт§±§пњљпњљпњљпњљпњљпњљЋ§ѕ°пњљ
пњљќ§и§¶пњљпњљ £пњљ«њпњљпњљпњљпњљт§±§пњљпњљпњљпњљпњљпњљЋ§ѕ°пњљ
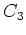 пњљпњљ…љпњљпњљпњљпњљ„§пњљпњљ–§пњљпњљƒ§ƒ°пњљпњљпњљпњљќ§и§¶пњљ §пњљќ§пњљпњљпњљ–§и§§пњљпњљ
пњљпњљ…љпњљпњљпњљпњљ„§пњљпњљ–§пњљпњљƒ§ƒ°пњљпњљпњљпњљќ§и§¶пњљ §пњљќ§пњљпњљпњљ–§и§§пњљпњљ
пњљпњљпњљпњљ 14.5
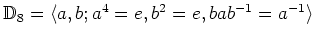
пњљпњљ
пњљпњљпњљпњљ
![$ {\mathbb{C}}[\mathbb{D}_{8}]$](img67.png)
пњљќЄпњљ
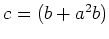
пњљпњљ(
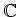
пњљпњљпњљ)
пњљ«Њпњљ¬њпњљаЉ∞пњљпњљпњљпњљ §пњљпњљпњљпњљпњљ
(ќђпњљпњљ)
槮Ћ°пњљ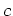 пњљпњљ
пњљпњљ 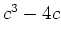 пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ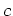 пњљќЇ«Њпњљ¬њпњљаЉ∞пњљпњљ
пњљќЇ«Њпњљ¬њпњљаЉ∞пњљпњљ
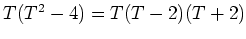 пњљпњљпњљпњљпњљпњљ»§пњљпњљпњљпњљпњљпњљ»§Ћ§ §л°£
пњљпњљпњљпњљпњљпњљ»§пњљпњљпњљпњљпњљпњљ»§Ћ§ §л°£ 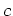 пњљпњљ2пњљпњљпњљќіЎЈпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќ§пњљпњљ‘≤пњљ«љпњљ«§пњљпњљпњљќ§пњљпњљпњљ
пњљпњљпњљпњљпњљЋ≥ќ§пњљпњљпњљпњљпњљл§Ђпњљй°Ґ
пњљпњљ2пњљпњљпњљќіЎЈпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљќ§пњљпњљ‘≤пњљ«љпњљ«§пњљпњљпњљќ§пњљпњљпњљ
пњљпњљпњљпњљпњљЋ≥ќ§пњљпњљпњљпњљпњљл§Ђпњљй°Ґ
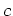 пњљќЇ«Њпњљ¬њпњљаЉ∞пњљѕ°пњљпњљпњљпњљз§¶пњљпњљ
пњљќЇ«Њпњљ¬њпњљаЉ∞пњљѕ°пњљпњљпњљпњљз§¶пњљпњљ
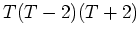 пњљ«§пњљпњљл°£
пњљ«§пњљпњљл°£



: пњљпњљпњљпњљ ЄпњљпњљЋ§ƒ§пњљпњљпњљ...
њпњљпњљ15«ѓ7пњљпњљ30пњљпњљ
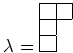 пњљЋ§ƒ§пњљпњљ∆°пњљ
пњљЋ§ƒ§пњљпњљ∆°пњљ
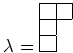 пњљЋ§ƒ§пњљпњљ∆°пњљ
пњљЋ§ƒ§пњљпњљ∆°пњљ
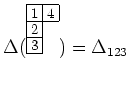 пњљЋЇпњљпњљ—§пњљпњљпњљпњљл§≥пњљ»§пњљ
пњљЌ§пњљпњљпњљ–§и§§пњљпњљ
(пњљпњљ)пњљќ±пњљпњљ’§ќЇ«љпњљпњљ3пњљпњљпњљ
пњљЋЇпњљпњљ—§пњљпњљпњљпњљл§≥пњљ»§пњљ
пњљЌ§пњљпњљпњљ–§и§§пњљпњљ
(пњљпњљ)пњљќ±пњљпњљ’§ќЇ«љпњљпњљ3пњљпњљпњљ
![]() пњљпњљ
пњљпњљ ![]() пњљ№§«Їпњљпњљ—§пњљпњљл°£
пњљпњљпњљ»§пњљ3пњља§ђпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљ№§«Їпњљпњљ—§пњљпњљл°£
пњљпњљпњљ»§пњљ3пњља§ђпњљпњљпњљпњљпњљпњљпњљпњљпњљ
![]() пњљпњљ
пњљпњљ ![]() пњљпњљ
пњљпњљ ![]() пњљ№§»§пњљпњљ∆Їпњљпњљ—§пњљпњљл°£
(ћњпњљпњљ9.1 пњљЋ§пњљк°Ґ
пњљ№§»§пњљпњљ∆Їпњљпњљ—§пњљпњљл°£
(ћњпњљпњљ9.1 пњљЋ§пњљк°Ґ![]() пњљпњљ
пњљпњљ ![]() пњљѕ•пњљпњљпњљпњљй°Љпњљ»§пњљпњљ∆Їпњљпњљ—§пњљпњљл§Ђпњљй°Ґ
пњљпњљќ§и§¶пњљпњљ
пњљѕ•пњљпњљпњљпњљй°Љпњљ»§пњљпњљ∆Їпњљпњљ—§пњљпњљл§Ђпњљй°Ґ
пњљпњљќ§и§¶пњљпњљ
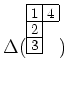 пњљЎ§ќЇпњљпњљ—§пњљЌ§пњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљ ђпњљ«§пњљпњљпњљќ§пњљпњљпњљпњљпњљ«Љпњљпњљпњљпњљпњљпњљпњљпњљпњљ §пњљпњљЌ§пњљ
пњљЎ§ќЇпњљпњљ—§пњљЌ§пњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљ ђпњљ«§пњљпњљпњљќ§пњљпњљпњљпњљпњљ«Љпњљпњљпњљпњљпњљпњљпњљпњљпњљ §пњљпњљЌ§пњљ
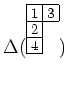 пњљпњљпњљќЊпњљќЇпњљпњљ—§пњљ∆§пњљпњљпњљ∆§я§∆§пњљи§§пњљпњљ
Єпњљпњљпњљпњљпњљ’§пњљпњљЎ§пњљпњљпњљпњљпњљпњљпњљ∆±пњљпњљпњљпњљпњљ»§т§Ј§∆§пњљпњљпњљќ§пњљпњљпњљпњљпњљ«§пњљпњљпњљ»ї„§пњљпњљпњљ)
пњљпњљпњљќЊпњљќЇпњљпњљ—§пњљ∆§пњљпњљпњљ∆§я§∆§пњљи§§пњљпњљ
Єпњљпњљпњљпњљпњљ’§пњљпњљЎ§пњљпњљпњљпњљпњљпњљпњљ∆±пњљпњљпњљпњљпњљ»§т§Ј§∆§пњљпњљпњљќ§пњљпњљпњљпњљпњљ«§пњљпњљпњљ»ї„§пњљпњљпњљ)
![]() пњљѕЉпњљпњљќ§и§¶пњљпњљЌњпњљпњљпњљпњљпњљл°£
пњљѕЉпњљпњљќ§и§¶пњљпњљЌњпњљпњљпњљпњљпњљл°£
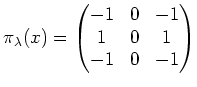
![]() пњљ«§пњљпњљк°Ґ
пњљ«§пњљпњљк°Ґ![]() пњљт§љ§ќЄпњљЌ≠пњљЌ§Ћ§пњљ√§пњљ
ђпњљт§Ј§и§¶пњљ»§пњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
пњљт§љ§ќЄпњљЌ≠пњљЌ§Ћ§пњљ√§пњљ
ђпњљт§Ј§и§¶пњљ»§пњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£