


: ïŋ―ïŋ―ïŋ―ïŋ―Ęļïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―...
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―IIïŋ―ïŋ―ïŋ―ïŋ― No.11
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĨÆĄïŋ―ïŋ―ïŋ―:
![\fbox{
·ēīÄ ${\mathbb {C}}[G]$ ĪÎīÄĪČĪ·ĪÆĪÎđ―ÂĪ
}](img1.png)
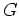 ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æĩïŋ―ïŋ―ëĪŋïŋ―ïŋ―ηïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æĩïŋ―ïŋ―ëĪŋïŋ―ïŋ―ηïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 11.1
![$ {\mathbb{C}}[G]$](img3.png)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
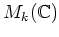
ïŋ―Îīïŋ―ïŋ―ÄĪïŋ―ïŋ―ïŋ―Äūïŋ―ŅĪČīÄĪČĪïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
![$ {\mathbb{C}}[G]$](img3.png) ïŋ―ïŋ―ïŋ―æŋīïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ÍĘŽïŋ―ōĪđĪëĪģïŋ―ČĪËĪïŋ―ÃĪÆĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ïžïŋ―ïŋ―ïŋ―
Ėŋïŋ―ïŋ―Ëĩïŋ―ïŋ―åĪĩïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―æŋīïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ÍĘŽïŋ―ōĪđĪëĪģïŋ―ČĪËĪïŋ―ÃĪÆĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ïžïŋ―ïŋ―ïŋ―
Ėŋïŋ―ïŋ―Ëĩïŋ―ïŋ―åĪĩïŋ―ïŋ―ëĄĢ
Ėŋïŋ―ïŋ― 11.2
ïŋ―ïŋ―ïŋ―Íïŋ―žïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―
-
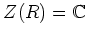
- ïŋ―ïŋ―ïŋ―ÆĪΚïŋ―
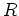 -ïŋ―÷ïŋ―ïŋ―Ïīïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
-ïŋ―÷ïŋ―ïŋ―Ïīïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÐĄïŋ―
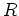
ïŋ―ÏĪïŋ―ïŋ―ëĨĩïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
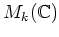
ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ËĪĘĪëĄĢ
ïŋ―ÂĪÏĄïŋ―Ėŋïŋ―ïŋ―11.2ïŋ―ïŋ―(2)ïŋ―Îēïŋ―ïŋ―ïŋ―ÎĪïŋ―ČĪĮĪÏĄïŋ―
ïŋ―æŋīïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ÍĘŽïŋ―ïŋ―ÏĄïŋ―ÎūÂĶïŋ―ïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ĘŽïŋ―ïŋ―ĮĪâĪĒïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ėĪŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ― 11.1
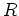
ïŋ―ïŋ―Ėŋïŋ―ïŋ―
11.2ïŋ―ïŋ―(2)ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
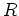
ïŋ―ïŋ―ĮĪïŋ―ÕĪïŋ―(ÎūÂĶ)ïŋ―ïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―
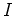
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
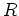
ïŋ―ÎĪïŋ―ïŋ―ïŋ―(ÎūÂĶ)ïŋ―ïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―
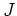
ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ÆĄïŋ―
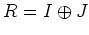
ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĄïŋ―
ïŋ―ČĪïŋ―ïŋ―ËĄïŋ―
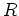
ïŋ―ïŋ―Ėŋïŋ―ïŋ―
11.2ïŋ―Îūïŋ―ïŋ―(1),(2)ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÐĄïŋ―
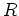
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ÎūÂĶ)ïŋ―ïŋ―ïŋ―ĮĨïŋ―ïŋ―ëĪŽÂļïŋ―ßĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―
Ėŋïŋ―ïŋ―11.2ïŋ―Îūïŋ―ïŋ―ïŋ―ïŋ―ËĪÏĪïŋ―ïŋ―ïŋ―Âūïŋ―Ë°Ęēïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ëĄĢ
ïŋ―ÝĨïŋ―ïŋ―ïŋ―ČĪÏĄïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―Ęūïŋ―ïž°(1),(2)ïŋ―ïŋ―ïŋ―éĪĪïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―Æīïŋ―ïŋ―Üđïŋ―ïŋ―ïŋ― 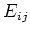 ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪōļŦĪÄĪïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĪŦïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪōļŦĪÄĪïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĪŦïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ― 11.2
ïŋ―ïŋ―
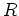
ïŋ―Κïŋ―ïŋ―ïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―
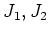
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆĄïŋ―
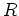
ïŋ―ïŋ―(
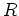
-ïŋ―ïŋ―ïŋ―÷ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―)
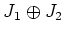
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ÐĄïŋ―
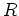
ïŋ―Îļïŋ―
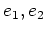
ïŋ―ĮĄïŋ―
ïŋ―ïŋ―ïŋ―Îūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ÍĢïŋ―ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ëĄĢ
-
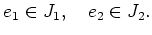
-
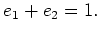
-
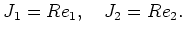
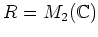 ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
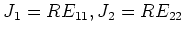 ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―É―ÅŠïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―É―ÅŠïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―Ęēïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËšŲĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Üđïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―ïŋ―ČĪËĪĘĪëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îūïŋ―ïŋ―ïŋ―ïŋ―ÏĪÉĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ōĪĪĪÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ŲĪïŋ―ïŋ―ïŋ―ïŋ―ÃĪËĪĘĪëĪ·ïŋ―ïŋ―ïŋ―ÜšŲĪïŋ―ïŋ―ÎĪęĪŋïŋ―ïŋ―ïŋ―ÍĪÏĪāĪ·ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÏĪĮđÍĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ÎĪĮĄïŋ―
ïŋ―ïŋ―ïŋ―ŲĪÆąé―Žïŋ―ïŋ―ïŋ―ïŋ―ËĪÞĪïĪđïŋ―ïŋ―ïŋ―ČĪËĪïŋ―ïŋ―ëĄĢ
ïŋ―ÞĪïŋ―ïŋ―ïŋ―
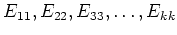 ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 11.3
Ėŋïŋ―ïŋ―
11.2ïŋ―Îēïŋ―ïŋ―ïŋ―ÎĪïŋ―ČĪĮĄïŋ―
-
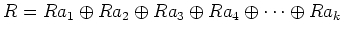 ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ― 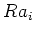 ïŋ―Ïīïŋ―ïŋ―ïŋ―
ïŋ―Ïīïŋ―ïŋ―ïŋ―
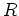 -ïŋ―÷ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―
-ïŋ―÷ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―
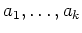 ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ëĄĢ
- ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―
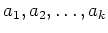 ïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŲĪëĄĢ
-
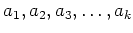 ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĄïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĄïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
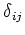 ïŋ―ÏĨïŋ―ïŋ―ïŋ―ïŋ―ÍĨÃĨïŋ―ïŋ―ÎĨĮĨëĨŋïŋ―ïŋ―)
ïŋ―ÏĨïŋ―ïŋ―ïŋ―ïŋ―ÍĨÃĨïŋ―ïŋ―ÎĨĮĨëĨŋïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ― 11.4
ïŋ―åĩïŋ―ïŋ―ïŋ―ïŋ―Îēïŋ―ïŋ―ïŋ―Îļïŋ―ïŋ―ĮĄïŋ―
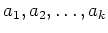
ïŋ―ïŋ―(1) ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(2)ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĪčĪĶïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
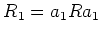
ïŋ―ÏīÄĪËĪĘĪęĄĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―(
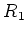
ïŋ―ïŋ―
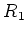
-ïŋ―ïŋ―ĘŽïŋ―÷ïŋ―)ïŋ―ïŋ―âĪŋïŋ―ĘĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 11.5
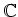
ïŋ―ïŋ―Íïŋ―žïŋ―ïŋ―ïŋ―ïŋ―Îīïŋ―
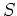
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ęšïŋ―ïŋ―ïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ïŋ―âĪŋïŋ―ĘĪïŋ―ïŋ―ĘĪïŋ―ÐĄïŋ―
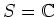
ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ÃĪËĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
11.4ïŋ―ïŋ―
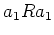
ïŋ―ïŋ―
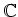
ïŋ―Ë°ïŋ―ïŋ―ŨĪïŋ―ïŋ―ëĄĢ
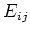 ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―11.7ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―11.7ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ÆĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―11.1ïŋ―ËĪïŋ―ęĄĒ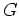 ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―Äīïŋ―ŲĪëĪģïŋ―ČĪËĩïŋ―ïŋ―åĪĩïŋ―ïŋ―ëĄĢïŋ―ÂĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―É―ïŋ―ïŋ―ïŋ―ÏļÂĪïŋ―ėĪŋïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―Äīïŋ―ŲĪëĪģïŋ―ČĪËĩïŋ―ïŋ―åĪĩïŋ―ïŋ―ëĄĢïŋ―ÂĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―É―ïŋ―ïŋ―ïŋ―ÏļÂĪïŋ―ėĪŋïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 11.3
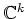
ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
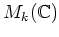
-ïŋ―÷ïŋ―ïŋ―Čļïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ōĪģĪïŋ―ïŋ―ĮĪïŋ―
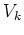
ïŋ―Č―ņĪŊĪČĄïŋ―
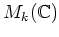
ïŋ―ïŋ―ĮĪïŋ―ÕĪïŋ―Íïŋ―žïŋ―ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―
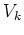
ïŋ―ïŋ―Íïŋ―ÂļÄĪïŋ―Äūïŋ―ÂĪïŋ―(
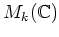
ïŋ―÷ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―)
Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ ïŋ―ČĪïŋ―ïŋ―ËĄïŋ―
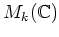
ïŋ―ïŋ―Íïŋ―žïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―ÉŽïŋ―ïŋ―
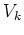
ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ― 11.1
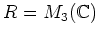
ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
11.3 ïŋ―Îūïŋ―ïŋ―(1),(2),(3)ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
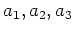
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
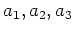
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
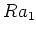
,
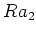
,
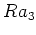
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪŋïŋ―ïŋ―Îūïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―Ë―ņĪąĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 11.2
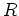
ïŋ―Κïŋ―
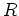
-ïŋ―ïŋ―ĘŽïŋ―÷ïŋ―(ïŋ―ÄĪÞĪęĄĒ
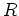
ïŋ―Κïŋ―ïŋ―ïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―)
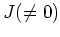
ïŋ―ïŋ―
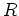
-ïŋ―÷ïŋ―ïŋ―ČĪïŋ―ïŋ―Æīïŋ―ïŋ―ïŋ―ĘĪïŋ―ÐĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―
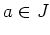
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆĄïŋ―
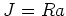
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĪïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ïŋ―
(ïŋ―ŌĨïŋ―ïŋ―:
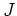
ïŋ―ïŋ―ĮĪïŋ―ÕĪÎļïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―
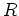
ïŋ―Κïŋ―ïŋ―ïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ )
ïŋ―ïŋ―ïŋ―ïŋ― 11.3
ïŋ―ïŋ―ïŋ―ïŋ―
11.3 ïŋ―ïŋ―(1),(2) ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĪčĪĶïŋ―ïŋ―
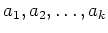
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(3)ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĪïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ïŋ―
(ïŋ―ŌĨïŋ―ïŋ―:
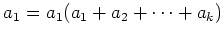
ïŋ―Îąïŋ―ïŋ―ÕĪïŋ―Åļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îūïŋ―ÕĪïŋ―ĘŽïŋ―ïŋ―(1)ïŋ―ïŋ―
ïŋ―ØĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ÓĪïŋ―ïŋ―čĄĢ
ïŋ―ïŋ―ïŋ―ïŋ― 11.4
ïŋ―ïŋ―ïŋ―ïŋ―
11.3ïŋ―Îēïŋ―ïŋ―ïŋ―ÎĪïŋ―ČĪïŋ―
ïŋ―ÉĪïŋ―
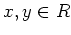
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪâĄĒ
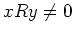
ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĄïŋ―
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
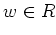
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪïŋ―
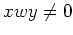
ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ŌĨïŋ―ïŋ―:
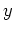
ïŋ―ïŋ―ïŋ―Äļïŋ―ïŋ―ęĪđïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―
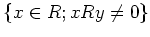
ïŋ―ïŋ―
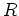
ïŋ―ïŋ―ÎūÂĶ
ïŋ―ïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ËĪĘĪëĄĢ)
ïŋ―ïŋ―ïŋ―ïŋ― 11.5
ïŋ―ïŋ―
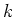
ïŋ―ïŋ―Íïŋ―žïŋ―ïŋ―ïŋ―ïŋ―Îīïŋ―
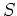
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ęšïŋ―ïŋ―ïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ïŋ―âĪŋïŋ―ĘĪïŋ―ïŋ―Čēïŋ―ïŋ―ęĪđïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
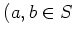
ïŋ―ïŋ―ïŋ―ïŋ―
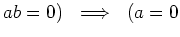
ïŋ―ÞĪïŋ―ïŋ―ïŋ―
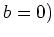
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĪïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ŌĨïŋ―ïŋ―:
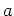
ïŋ―ïŋ― 0 ïŋ―ĮĪĘĪïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ČĄïŋ―
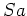
ïŋ―ïŋ―
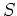
ïŋ―Κïŋ―ïŋ―ïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―ĮĄïŋ―0 ïŋ―ĮĪÏĪĘĪïŋ―ïŋ―ïŋ―ïŋ―éĄĒ
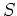
ïŋ―ËĪĘĪéĪķïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
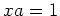
ïŋ―ĘĪïŋ―
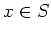
ïŋ―ïŋ―Âļïŋ―ßĪïŋ―Æģïŋ―ïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ― 11.6
ïŋ―ïŋ―ïŋ―ïŋ―
11.5ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ(ïŋ―ŌĨïŋ―ïŋ―:ĮĪïŋ―ÕĪïŋ―
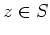
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
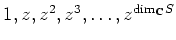
ïŋ―Ï°ėžĄïŋ―ïŋ―ÎĐïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―áĄĒ
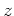
ïŋ―ïŋ―
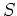
ïŋ―åĪĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Įūïŋ―ïŋ―ÎĪïŋ―ïŋ―(
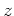
ïŋ―ΚĮūïŋ―Âŋïŋ―āž°) ïŋ―ïŋ―
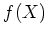
ïŋ―ČĪïŋ―ïŋ―ïŋ―ČĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ØĪÎīïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―
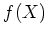
ïŋ―ïŋ―
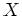
ïŋ―ΰėžĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ĘŽïŋ―ōĪđĪëĄĢïŋ―ÄĪÞĪęĄĒ
ïŋ―ĘĪïŋ―
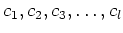
ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ)
ïŋ―ïŋ―ïŋ―ïŋ― 11.7
ïŋ―ïŋ―ïŋ―ïŋ―
11.3ïŋ―Îēïŋ―ïŋ―ïŋ―ÎĪïŋ―ČĪĮĄïŋ―
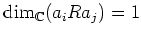
ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ŌĨïŋ―ïŋ―: ïŋ―ïŋ―ïŋ―ïŋ―
11.4ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ÆĄïŋ―0 ïŋ―Č°ÛĪĘĪïŋ―čĪĶïŋ―ïŋ―
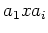
,
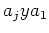
ïŋ―ïŋ―ïŋ―ÕĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÆĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
11.5 ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ëĄĢ)



: ïŋ―ïŋ―ïŋ―ïŋ―Ęļïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―...
2003/7/5
![]() ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æĩïŋ―ïŋ―ëĪŋïŋ―ïŋ―ηïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æĩïŋ―ïŋ―ëĪŋïŋ―ïŋ―ηïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![$\displaystyle {\mathbb{C}}[G]\cong \prod_{i=1}^\ell M_{k_i}({\mathbb{C}})
$](img5.png)
![]() ïŋ―ïŋ―ïŋ―æŋīïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ÍĘŽïŋ―ōĪđĪëĪģïŋ―ČĪËĪïŋ―ÃĪÆĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ïžïŋ―ïŋ―ïŋ―
Ėŋïŋ―ïŋ―Ëĩïŋ―ïŋ―åĪĩïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―æŋīïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ÍĘŽïŋ―ōĪđĪëĪģïŋ―ČĪËĪïŋ―ÃĪÆĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ïžïŋ―ïŋ―ïŋ―
Ėŋïŋ―ïŋ―Ëĩïŋ―ïŋ―åĪĩïŋ―ïŋ―ëĄĢ
![]() ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪōļŦĪÄĪïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĪŦïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪōļŦĪÄĪïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĪŦïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ëĄĢ
![]() ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
![]() ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―É―ÅŠïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―É―ÅŠïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
![]() ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―
![]() ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―Äīïŋ―ŲĪëĪģïŋ―ČĪËĩïŋ―ïŋ―åĪĩïŋ―ïŋ―ëĄĢïŋ―ÂĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―É―ïŋ―ïŋ―ïŋ―ÏļÂĪïŋ―ėĪŋïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―Äīïŋ―ŲĪëĪģïŋ―ČĪËĩïŋ―ïŋ―åĪĩïŋ―ïŋ―ëĄĢïŋ―ÂĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―É―ïŋ―ïŋ―ïŋ―ÏļÂĪïŋ―ėĪŋïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―