


: ïŋ―ïŋ―ïŋ―ïŋ―Ęļïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―...
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―II ïŋ―ïŋ―ïŋ―ïŋ― No.13
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĨÆĄïŋ―ïŋ―ïŋ―:

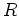 ïŋ―ÏīÄĪĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―ÏīÄĪĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ― 13.1
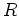
ïŋ―÷ïŋ―
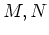
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
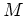
ïŋ―ïŋ―ïŋ―ïŋ―
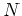
ïŋ―ØĪïŋ―
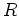
-ïŋ―÷ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―
ïŋ―Č―ņĪŊĄïŋ―
ïŋ―Ęēïŋ―ïŋ―ïŋ―
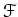 ïŋ―ïŋ―ÅŽïŋ―ïŋ―ïŋ―ĘīØŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ãĪĻïŋ―ÐĄïŋ―
ïŋ―ïŋ―ÅŽïŋ―ïŋ―ïŋ―ĘīØŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ãĪĻïŋ―ÐĄïŋ―
![$ {\mathbb{C}}[[x]]$](img8.png) ïŋ―ōĪĒĪïŋ―ïĪđïŋ―ïŋ―ïŋ―ČĪËĪïŋ―ïŋ―ëĄĢ
ïŋ―ōĪĒĪïŋ―ïĪđïŋ―ïŋ―ïŋ―ČĪËĪïŋ―ïŋ―ëĄĢ
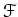 ïŋ―ïŋ―
ïŋ―ïŋ―
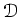 ïŋ―Κïŋ―ïŋ―ŅĪËĪÄĪïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―.
ïŋ―Κïŋ―ïŋ―ŅĪËĪÄĪïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―.
ïŋ―ïŋ―ïŋ―ïŋ― 13.1
ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪÎĪĘĪïŋ―ïŋ―ïŋ―
![$ \mathcal D ={\mathbb{C}}[x,\partial_x]$](img10.png)
ïŋ―ČĄïŋ―ïŋ―ïŋ―ïŋ―ΰïŋ―ÄĪÎļïŋ―
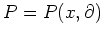
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
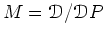
ïŋ―Ï°ïŋ―ÄĪïŋ―
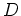
-
ïŋ―÷ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ ïŋ―Øŋïŋ―ïŋ―ïŋ―
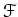
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―
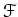
ïŋ―ĮĪïŋ―
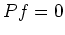
ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îēïŋ―Îķïŋ―ïŋ―ÖĪïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ― 13.2
ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪÎĪĘĪïŋ―ïŋ―ïŋ―
![$ \mathcal D ={\mathbb{C}}[x,\partial_x]$](img10.png)
ïŋ―ČĄïŋ―ïŋ―ïŋ―ïŋ―ΰïŋ―ÄĪÎļïŋ―
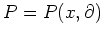
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ÍĪïŋ―
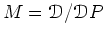
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
-
ïŋ―ĘĪëī°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ëĄĢ
- ïŋ―ïŋ―Îīïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―óĪŦĪïŋ―
ïŋ―ĘĪëī°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ėĄĒïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―Îīïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
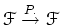 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÍĪĮĪÏĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ÂĪÏĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÍĪĮĪÏĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ÂĪÏĄïŋ―
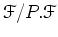 ïŋ―ÏĨÛĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Įļïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÏĨÛĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Įļïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
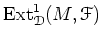 ïŋ―Ë°ïŋ―ïŋ―ŨĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―Îĩïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ņŋïŋ―ïŋ―Ëļïŋ―ïŋ―ęĪ·ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢ
Âŋïŋ―Ņŋïŋ―ïŋ―ïŋ―ïŋ―ČĪÉĪïŋ―ïŋ―ĘĪïŋ―ÎĪïŋ―ïŋ―äĄĒïŋ―ÜšŲĪËĪÄĪïŋ―ïŋ―ÆĪïŋ―
ïŋ―ÜđÖĩïŋ―ïŋ―Îŧïŋ―ïŋ―Í―ïŋ―ËĩóĪēĪïŋ―ïŋ―Öē÷ïŋ―ïŋ―ïŋ―ïŋ―ÃĄŨĪËūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Ë°ïŋ―ïŋ―ŨĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―Îĩïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ņŋïŋ―ïŋ―Ëļïŋ―ïŋ―ęĪ·ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢ
Âŋïŋ―Ņŋïŋ―ïŋ―ïŋ―ïŋ―ČĪÉĪïŋ―ïŋ―ĘĪïŋ―ÎĪïŋ―ïŋ―äĄĒïŋ―ÜšŲĪËĪÄĪïŋ―ïŋ―ÆĪïŋ―
ïŋ―ÜđÖĩïŋ―ïŋ―Îŧïŋ―ïŋ―Í―ïŋ―ËĩóĪēĪïŋ―ïŋ―Öē÷ïŋ―ïŋ―ïŋ―ïŋ―ÃĄŨĪËūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ČĪęĪĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ïžïŋ―ïŋ―ÎĪïŋ―ïŋ―ČĪËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÕĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
Ėŋïŋ―ïŋ― 13.1
ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪÎĪĘĪïŋ―ïŋ―ïŋ―
![$ \mathcal D ={\mathbb{C}}[x,\partial_x]$](img10.png)
ïŋ―ČĄïŋ―ïŋ―ïŋ―ïŋ―ΰïŋ―ÄĪÎļïŋ―
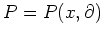
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
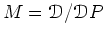
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Øŋïŋ―ïŋ―ïŋ―
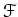
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĄïŋ―
ïŋ―ïŋ―ïŋ― 13.2
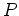
ïŋ―ïŋ―
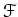
ïŋ―ïŋ―ÎĨïŋ―ïŋ―ïŋ―ĮĨÃĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ(ÃĒïŋ―ïŋ―ïŋ―ïŋ―ÄĪΞïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―Íïŋ―žïŋ―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ― 13.1
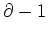
ïŋ―ïŋ―
![$ {\mathbb{C}}[[x]]$](img8.png)
ïŋ―ïŋ―ÎĨïŋ―ïŋ―ïŋ―ĮĨÃĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
Ęŋïŋ―ïŋ―16ĮŊ2ïŋ―ïŋ―19ïŋ―ïŋ―
![]()
![]() ïŋ―ÏīÄĪĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―ÏīÄĪĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
![]() ïŋ―ïŋ―ÅŽïŋ―ïŋ―ïŋ―ĘīØŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ãĪĻïŋ―ÐĄïŋ―
ïŋ―ïŋ―ÅŽïŋ―ïŋ―ïŋ―ĘīØŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―ãĪĻïŋ―ÐĄïŋ―
![]() ïŋ―ōĪĒĪïŋ―ïĪđïŋ―ïŋ―ïŋ―ČĪËĪïŋ―ïŋ―ëĄĢ
ïŋ―ōĪĒĪïŋ―ïĪđïŋ―ïŋ―ïŋ―ČĪËĪïŋ―ïŋ―ëĄĢ
![]() ïŋ―ïŋ―
ïŋ―ïŋ―
![]() ïŋ―Κïŋ―ïŋ―ŅĪËĪÄĪïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―.
ïŋ―Κïŋ―ïŋ―ŅĪËĪÄĪïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―.
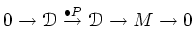
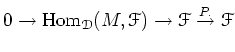
![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÍĪĮĪÏĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ÂĪÏĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÍĪĮĪÏĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ÂĪÏĄïŋ―
![]() ïŋ―ÏĨÛĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Įļïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÏĨÛĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Įļïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―Ë°ïŋ―ïŋ―ŨĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―Îĩïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ņŋïŋ―ïŋ―Ëļïŋ―ïŋ―ęĪ·ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢ
Âŋïŋ―Ņŋïŋ―ïŋ―ïŋ―ïŋ―ČĪÉĪïŋ―ïŋ―ĘĪïŋ―ÎĪïŋ―ïŋ―äĄĒïŋ―ÜšŲĪËĪÄĪïŋ―ïŋ―ÆĪïŋ―
ïŋ―ÜđÖĩïŋ―ïŋ―Îŧïŋ―ïŋ―Í―ïŋ―ËĩóĪēĪïŋ―ïŋ―Öē÷ïŋ―ïŋ―ïŋ―ïŋ―ÃĄŨĪËūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Ë°ïŋ―ïŋ―ŨĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―Îĩïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ņŋïŋ―ïŋ―Ëļïŋ―ïŋ―ęĪ·ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢ
Âŋïŋ―Ņŋïŋ―ïŋ―ïŋ―ïŋ―ČĪÉĪïŋ―ïŋ―ĘĪïŋ―ÎĪïŋ―ïŋ―äĄĒïŋ―ÜšŲĪËĪÄĪïŋ―ïŋ―ÆĪïŋ―
ïŋ―ÜđÖĩïŋ―ïŋ―Îŧïŋ―ïŋ―Í―ïŋ―ËĩóĪēĪïŋ―ïŋ―Öē÷ïŋ―ïŋ―ïŋ―ïŋ―ÃĄŨĪËūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―