


: ����ʸ��ˤĤ���...
���������II ���� No.9
�����Υơ���:

��ʬ�礭�ʴؿ�����(�㤨��
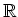 ���ʣ�ǿ���
���ʣ�ǿ��� 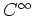 -�ؿ�������)��
��ĸ��ꤷ�ơ�
-�ؿ�������)��
��ĸ��ꤷ�ơ�
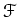 �Ƚ������Τ褦����ʬ�������������
�Ƚ������Τ褦����ʬ�������������
(
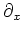 �Ȥ�
�Ȥ�
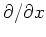 �Τ��ȡ��ʲ�Ʊ��)
������������
�Τ��ȡ��ʲ�Ʊ��)
������������
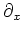 �Ȥ���
�Ȥ���
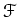 ������������Ǥ���
����
������������Ǥ���
��ζ��� 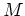 ���������ط����ȹͤ��뤳�Ȥ��Ǥ��롣
���������ط����ȹͤ��뤳�Ȥ��Ǥ��롣
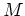 �ϼºݤ�
�ϼºݤ�
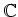 ��ͭ�¼����Ǥ��äơ����ޤǤ�����������μ���
���Ѥ��뤳�Ȥ��Ǥ��롣
��ͭ�¼����Ǥ��äơ����ޤǤ�����������μ���
���Ѥ��뤳�Ȥ��Ǥ��롣
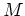 �ˤ�
�ˤ�
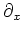 �����Ѥ��Ƥ��ơ�
�����Ѥ��Ƥ��ơ�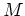 ��
��
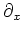 ��
�� 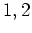 �Ȥ�����Ĥ�
��ͭ�ͤˤ���ͭʬ��롣
�Ȥ�����Ĥ�
��ͭ�ͤˤ���ͭʬ��롣
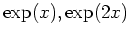 ����ͭ�٥��ȥ�Ǥ��롣
����ͭ�٥��ȥ�Ǥ��롣
Ʊ�ͤ�
�ˤĤ��Ƥ��������Ū�ʲ��Ǥ��롣
���٤ϲ���־�
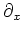 �θ�ͭ�ͤ���ʣ���ƽФƤ���Ȥ��������դ�ɬ�פǤ��롣
�θ�ͭ�ͤ���ʣ���ƽФƤ���Ȥ��������դ�ɬ�פǤ��롣
�ⳬ�����������㤨��
�Ǥ�����Ʊ���Ǥ��롣
ʿ��15ǯ12��1��
![]()
![]() ���ʣ�ǿ���
���ʣ�ǿ��� ![]() -�ؿ�������)��
��ĸ��ꤷ�ơ�
-�ؿ�������)��
��ĸ��ꤷ�ơ�
![]() �Ƚ������Τ褦����ʬ�������������
�Ƚ������Τ褦����ʬ�������������
![]() �ˤ�
�ˤ�
![]() �����Ѥ��Ƥ��ơ�
�����Ѥ��Ƥ��ơ�![]() ��
��
![]() ��
�� ![]() �Ȥ�����Ĥ�
��ͭ�ͤˤ���ͭʬ��롣
�Ȥ�����Ĥ�
��ͭ�ͤˤ���ͭʬ��롣