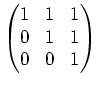: ïŋ―ïŋ―ïŋ―ïŋ―Ęļïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―...
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―II ïŋ―ïŋ―ïŋ―ïŋ― No.4
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĨÆĄïŋ―ïŋ―ïŋ―:

ïŋ―č―ĩïŋ―Ë°ïŋ―ïŋ―ïŋ―Âģïŋ―ïŋ―ïŋ―ïŋ―
 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
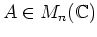 ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ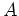 ïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―Ëšïŋ―ïŋ―ŅĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪïŋ―ïŋ―čĪĶïŋ―ËĄïŋ―ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ― 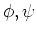 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ÃĒïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ÃĒïŋ―ïŋ―ïŋ―ïŋ― 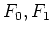 ïŋ―ÏĨïŋ―ÎĪČĪïŋ―ïŋ―ÆĪïŋ―Æąïŋ―ïŋ―ïŋ―ĮĄïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ÏĨïŋ―ÎĪČĪïŋ―ïŋ―ÆĪïŋ―Æąïŋ―ïŋ―ïŋ―ĮĄïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
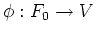 ïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―ĮĄïŋ― 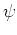 ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―Ęžïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ÃĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―Ęžïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ÃĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÏĄïŋ―ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ōĪĪĪÆĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
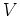 ïŋ―ÎģÆļïŋ―ïŋ―ïŋ―ĘĢïŋ―Įŋïŋ―ïŋ―ÜĪïŋ―ïŋ―ÂĪïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―
ïŋ―ÎģÆļïŋ―ïŋ―ïŋ―ĘĢïŋ―Įŋïŋ―ïŋ―ÜĪïŋ―ïŋ―ÂĪïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―
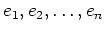 ïŋ―ĮĪïŋ―ïŋ―ÞĪïŋ―É―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ÞĪïŋ―É―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
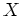 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―ČĪÉĪÎĪïŋ―ïŋ―éĪĪïŋ―ïŋ―ïŋ―ÞĪïŋ―É―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―ČĪÉĪÎĪïŋ―ïŋ―éĪĪïŋ―ïŋ―ïŋ―ÞĪïŋ―É―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―č―ĩïŋ―ïŋ―Ãąïŋ―ïŋ―ïŋ―ŌĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―Ãąïŋ―ïŋ―Ęēïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 4.1
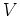
ïŋ―ïŋ―
![$ {\mathbb{C}}[X]$](img21.png)
-ïŋ―÷ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
![$ {\mathbb{C}}[X]/d(X){\mathbb{C}}[X]$](img22.png)
ïŋ―ηïŋ―ïŋ―Îē÷ïŋ―ïŋ―ïŋ―
Äūïŋ―ÂĪïŋ―Æąïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ČĪïŋ―ïŋ―ËĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÖĪÏĄïŋ―
![$ {\mathbb{C}}[X]/X^k {\mathbb{C}}[X]$](img23.png) ïŋ―ηïŋ―ïŋ―Îē÷ïŋ―ïŋ―ïŋ―
Äūïŋ―ÂĪïŋ―ĘŽïŋ―ōĪĩĪïŋ―ëĄĢ
ïŋ―ηïŋ―ïŋ―Îē÷ïŋ―ïŋ―ïŋ―
Äūïŋ―ÂĪïŋ―ĘŽïŋ―ōĪĩĪïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îļïŋ―ïŋ―ÕĪĮ―ņĪŊĪČĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Éļïŋ―ā·ŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―óĪēĪčĪĶïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ëĄĢ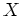 ïŋ―ïŋ―
ïŋ―ïŋ―
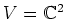 ïŋ―ØĪΚïŋ―ïŋ―ŅĪïŋ―
ïŋ―ØĪΚïŋ―ïŋ―ŅĪïŋ― 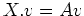 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―Ïžïŋ―ïŋ―ÎĪčĪĶïŋ―Ęđïŋ―ïŋ―óŧŧĪïŋ―É―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―Ïžïŋ―ïŋ―ÎĪčĪĶïŋ―Ęđïŋ―ïŋ―óŧŧĪïŋ―É―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
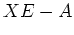 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪïŋ―ïŋ―čĪĶïŋ―ïŋ―
ïŋ―Č―ņĪĪĪÆĪßĪëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪïŋ―ïŋ―čĪĶïŋ―ïŋ―
ïŋ―Č―ņĪĪĪÆĪßĪëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
![$ {\mathbb{C}}[X]$](img21.png) -ïŋ―÷ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĪïŋ―
-ïŋ―÷ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĪïŋ― 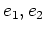 ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ėĄĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ĮĪïŋ―ïŋ―ïŋ―
ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ėĄĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ĮĪïŋ―ïŋ―ïŋ― 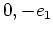 ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪËĪĘĪëĄĢ
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪËĪĘĪëĄĢ
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
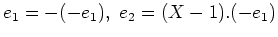 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪËĪïŋ―ïŋ―ïŋ―ïŋ―ÕĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪËĪïŋ―ïŋ―ïŋ―ïŋ―ÕĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Øŋïŋ―ïŋ―ïŋ―ïŋ―ß·ŨĄïŋ―
No2.ïŋ―ÎĨïŋ―ÝĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ïūïŋ―ïŋ―ïŋ―ïŋ―ņĪ·Īïŋ―ïŋ―ÃĪïŋ―ïŋ―čĪĶïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ÏĄïŋ―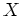 ïŋ―ÎīØŋïŋ―
ïŋ―ÎīØŋïŋ― 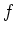 ïŋ―ĮĄïŋ―
ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ÎĪïŋ―ÄĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ëĄĢ
ïŋ―ĮĄïŋ―
ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ÎĪïŋ―ÄĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ëĄĢ
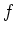 ïŋ―ïŋ―
ïŋ―ïŋ― 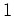 ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĄïŋ―
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĄïŋ―
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―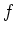 ïŋ―ïŋ―
ïŋ―ïŋ― 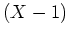 ïŋ―Įģïŋ―ïŋ―ïŋ―ÚĪïŋ―ëĄĢ
ïŋ―Įģïŋ―ïŋ―ïŋ―ÚĪïŋ―ëĄĢ
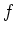 ïŋ―ÏĄïŋ―
ïŋ―ÏĄïŋ―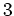 ïŋ―Įŧïŋ―ïŋ―ÅĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĄïŋ―
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Įŧïŋ―ïŋ―ÅĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĄïŋ―
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―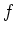 ïŋ―ïŋ―
ïŋ―ïŋ― 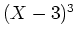 ïŋ―Įģïŋ―ïŋ―ïŋ―ÚĪïŋ―ëĄĢ
ïŋ―Įģïŋ―ïŋ―ïŋ―ÚĪïŋ―ëĄĢ
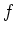 ïŋ―ÏĄïŋ―
ïŋ―ÏĄïŋ―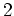 ïŋ―ïŋ― ïŋ―ïŋ―ÅĪÎĄïŋ―
ïŋ―ïŋ― ïŋ―ïŋ―ÅĪÎĄïŋ―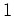 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĄïŋ―
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĄïŋ―
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―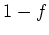 ïŋ―ïŋ―
ïŋ―ïŋ― 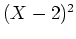 ïŋ―Įģïŋ―ïŋ―ïŋ―ÚĪïŋ―ëĄĢ
ïŋ―Įģïŋ―ïŋ―ïŋ―ÚĪïŋ―ëĄĢ
(Æąïŋ―ÍĪÎĪïŋ―ÎĪïŋ―3ïŋ―Äšïŋ―ïŋ―ÉŽïŋ―ŨĪïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ)
(ïŋ―ïŋ―)ïŋ―ïŋ―ÃĪČĪïŋ―ïŋ―ÚĪïŋ―ïŋ―ïŋ―ËĄïŋ―ÏĄïŋ―ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ËĪïŋ―ïŋ―ëĪģïŋ―ČĪĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
- Step 1..
-
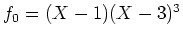 ïŋ―ïŋ―ÍĪïŋ―ïŋ―ëĄĢ (
ïŋ―ïŋ―ÍĪïŋ―ïŋ―ëĄĢ (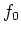 ïŋ―Ïūïŋ―ïŋ― (1),(2)ïŋ―Îūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)
ïŋ―Ïūïŋ―ïŋ― (1),(2)ïŋ―Îūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)
- Step 2..
-
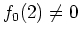 ïŋ―ĘĪÎĪĮĄïŋ―
ïŋ―ĘĪÎĪĮĄïŋ―
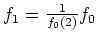 ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 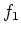 ïŋ―ïŋ― ïŋ―ïŋ―Îūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ― ïŋ―ïŋ―Îūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―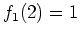 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢ
- Step 3..
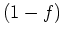 ïŋ―ïŋ―
ïŋ―ïŋ― 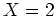 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪčĪĶïŋ―ĘīØŋïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ËĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪčĪĶïŋ―ĘīØŋïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ËĪïŋ― 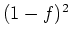 ïŋ―ČĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĪ·ïŋ―ÆĪïŋ―ïŋ―ÐĪčĪĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ÕĪïŋ―ïŋ―ëĄĢ
ïŋ―ČĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĪ·ïŋ―ÆĪïŋ―ïŋ―ÐĪčĪĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ÕĪïŋ―ïŋ―ëĄĢ
- Step 4..
-
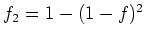 ïŋ―ïŋ―ÍĪïŋ―ïŋ―ïŋ―ÐĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ïūïŋ―Îūïŋ―ïŋ―(1),(2),(3)ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ÍĪïŋ―ïŋ―ïŋ―ÐĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ïūïŋ―Îūïŋ―ïŋ―(1),(2),(3)ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―ÏĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Øŋïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ÝūÚĪïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪŽïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ãīģïŋ―âĪŊïŋ―ĘĪïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĄïŋ―
(ïŋ―ïŋ―)
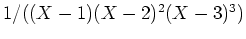 ïŋ―ïŋ―ïŋ―ïŋ―ĘŽĘŽïŋ―ïŋ―Åļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―âĪĒïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ĘŽĘŽïŋ―ïŋ―Åļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―âĪĒïŋ―ëĄĢ
ïŋ―ČĪïŋ―ÃĪÆĄïŋ―
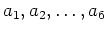 ïŋ―ïŋ―(Îąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âūïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―ïŋ―)ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―(Îąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âūïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―ïŋ―)ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 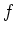 ïŋ―ïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪĮĪïŋ―ïŋ―ëĄĢïŋ―ãĪĻïŋ―ïŋ―
ïŋ―ïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪĮĪïŋ―ïŋ―ëĄĢïŋ―ãĪĻïŋ―ïŋ― 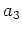 ïŋ―ōļĶĩæĪđïŋ―ïŋ―ËĪïŋ―
Îūïŋ―ÕĪïŋ―
ïŋ―ōļĶĩæĪđïŋ―ïŋ―ËĪïŋ―
Îūïŋ―ÕĪïŋ― 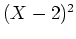 ïŋ―ïŋ―ÝĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ÝĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ― 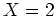 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ïŋ―ëĪĪïŋ―ÏĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ïŋ―ëĪĪïŋ―ÏĄïŋ―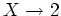 ïŋ―ÎķËļÂĪïŋ―ČĪïŋ―ïŋ―)ïŋ―čĪĪïŋ―ïŋ―
ïŋ―ÎķËļÂĪïŋ―ČĪïŋ―ïŋ―)ïŋ―čĪĪïŋ―ïŋ―
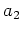 ïŋ―ïŋ― Îūïŋ―ÕĪïŋ―
ïŋ―ïŋ― Îūïŋ―ÕĪïŋ― 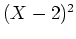 ïŋ―ïŋ―ÝĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Č°ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ÝĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Č°ïŋ―ïŋ―ïŋ― 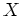 ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―ėĪŦïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―ėĪŦïŋ―ïŋ― 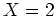 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪĮĪïŋ―ČĪïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪĮĪïŋ―ČĪïŋ―ïŋ―ïŋ―ëĄĢ
(ïŋ―ïŋ―) ïŋ―ïŋ―ïŋ―ïŋ―ÎđÖĩïŋ―ïŋ―ΚĮļïŋ―ËĪïŋ―ÃĪïŋ―ïŋ―čĪĶïŋ―ËĄïŋ―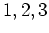 ïŋ―ĮĪïŋ―ïŋ―ėĪūïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ėĪūïŋ―ïŋ― 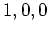 ,
, 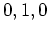 ,
, 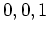 ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ÍĪïŋ―ČĪïŋ―čĪĶïŋ―ïŋ―Âŋïŋ―āž°
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ÍĪïŋ―ČĪïŋ―čĪĶïŋ―ïŋ―Âŋïŋ―āž°
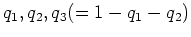 ïŋ―ïŋ―ČĪęĄĒ
ïŋ―ïŋ―ČĪęĄĒ
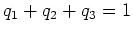 ïŋ―ïŋ―Îūïŋ―ÕĪÎđâĪĪïŋ―ŌĪïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Îūïŋ―ÕĪÎđâĪĪïŋ―ŌĪïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ÍĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―âĪĒïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÕĪïŋ―Åļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æ―ÐĪÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
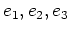 ïŋ―ÎĪÉĪėĪŦïŋ―ïŋ―ÄĪïŋ―ïŋ―įĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ÎĪĮĄïŋ―
ïŋ―ÎĪÉĪėĪŦïŋ―ïŋ―ÄĪïŋ―ïŋ―įĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ÎĪĮĄïŋ―
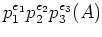 ïŋ―ïŋ―
ïŋ―ïŋ―
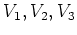 ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ėĪŦïŋ―ÎĪßĪïŋ― 0 ïŋ―Č°ÛĪĘĪïŋ―ïŋ―ÍĪïŋ―ČĪëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪËĩïŋ―ïŋ―ïŋ―Âŋïŋ―āž°ïŋ―ïŋ―
ïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïĪąïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ėĪŦïŋ―ÎĪßĪïŋ― 0 ïŋ―Č°ÛĪĘĪïŋ―ïŋ―ÍĪïŋ―ČĪëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪËĩïŋ―ïŋ―ïŋ―Âŋïŋ―āž°ïŋ―ïŋ―
ïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïĪąïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ― 4.1
ïŋ―ïŋ―ïŋ―Îđïŋ―ïŋ―ïŋ―ÎĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Éļïŋ―ā·ŋïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―



: ïŋ―ïŋ―ïŋ―ïŋ―Ęļïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―...
Ęŋïŋ―ïŋ―15ĮŊ11ïŋ―ïŋ―8ïŋ―ïŋ―
![]()
![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ![]() ïŋ―ïŋ―
ïŋ―ïŋ―
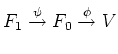
![% latex2html id marker 924
$\displaystyle F_0=F_1={\mathbb{C}}[X]^n
=\left\{
\...
..._n(X)
\end{pmatrix} ; a_i (X)\in {\mathbb{C}}[X] \quad(i=1,2,\dots,n)
\right\}
$](img9.png)
![]() ïŋ―ÎģÆļïŋ―ïŋ―ïŋ―ĘĢïŋ―Įŋïŋ―ïŋ―ÜĪïŋ―ïŋ―ÂĪïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―
ïŋ―ÎģÆļïŋ―ïŋ―ïŋ―ĘĢïŋ―Įŋïŋ―ïŋ―ÜĪïŋ―ïŋ―ÂĪïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―
![]() ïŋ―ĮĪïŋ―ïŋ―ÞĪïŋ―É―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ÞĪïŋ―É―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―ČĪÉĪÎĪïŋ―ïŋ―éĪĪïŋ―ïŋ―ïŋ―ÞĪïŋ―É―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―ČĪÉĪÎĪïŋ―ïŋ―éĪĪïŋ―ïŋ―ïŋ―ÞĪïŋ―É―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―ηïŋ―ïŋ―Îē÷ïŋ―ïŋ―ïŋ―
Äūïŋ―ÂĪïŋ―ĘŽïŋ―ōĪĩĪïŋ―ëĄĢ
ïŋ―ηïŋ―ïŋ―Îē÷ïŋ―ïŋ―ïŋ―
Äūïŋ―ÂĪïŋ―ĘŽïŋ―ōĪĩĪïŋ―ëĄĢ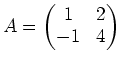
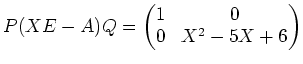
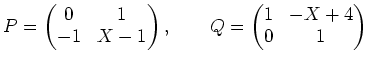
![]() ïŋ―ÎīØŋïŋ―
ïŋ―ÎīØŋïŋ― ![]() ïŋ―ĮĄïŋ―
ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ÎĪïŋ―ÄĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ëĄĢ
ïŋ―ĮĄïŋ―
ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ÎĪïŋ―ÄĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ëĄĢ
![]() ïŋ―ïŋ―ïŋ―ïŋ―ĘŽĘŽïŋ―ïŋ―Åļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―âĪĒïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ĘŽĘŽïŋ―ïŋ―Åļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―âĪĒïŋ―ëĄĢ
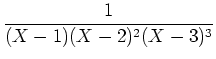
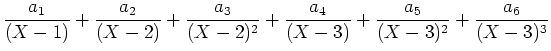
![]() ïŋ―ĮĪïŋ―ïŋ―ėĪūïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ėĪūïŋ―ïŋ― ![]() ,
, ![]() ,
, ![]() ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ÍĪïŋ―ČĪïŋ―čĪĶïŋ―ïŋ―Âŋïŋ―āž°
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ÍĪïŋ―ČĪïŋ―čĪĶïŋ―ïŋ―Âŋïŋ―āž°
![]() ïŋ―ïŋ―ČĪęĄĒ
ïŋ―ïŋ―ČĪęĄĒ
![]() ïŋ―ïŋ―Îūïŋ―ÕĪÎđâĪĪïŋ―ŌĪïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Îūïŋ―ÕĪÎđâĪĪïŋ―ŌĪïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―