鐃緒申鐃緒申鐃緒申鐃緒申鐃�II 鐃緒申鐃緒申 No.3

鐃緒申鐃緒申鐃塾テ￥申鐃緒申:

$\fbox{行列の単因子}$

鐃緒申鐃緒申鐃塾�申譴�申鐃峻わ申鐃夙￥申鐃緒申鐃緒申鐃緒申泙鐃緒申鐃緒申有鐃緒申鐃瞬わ申鐃夙わ申分鐃緒申鐃銃考わ申鐃銃￥申鐃緒申鐃曙ぞ鐃緒申鐃緒申鐃淑�申鐃� 鐃緒申標鐃準型鐃緒申佑鐃緒申鐃塾わ申鐃緒申鐃緒申鐃叔わ申鐃緒申里鐃緒申鐃緒申鐃� 鐃純干鐃緒申鐃緒申鐃薯かわ申鐃銃加件申鐃緒申鐃緒申鐃緒申鐃緒申鐃緒申鐃獣わ申覆鐃処う鐃緒申鐃緒申鐃緒申鐃緒申鐃緒申鐃緒申 $A \in M_n({\mathbb{C}})$ 鐃緒申与鐃緒申鐃緒申鐃銃わ申鐃緒申箸鐃緒申襦� 鐃緒申

$\displaystyle V={\mathbb{C}}^n ={\mathbb{C}}e_1+{\mathbb{C}}e_2 + {\mathbb{C}}e_3+\dots {\mathbb{C}}e_n$

鐃祝削申鐃術わ申鐃暑。但鐃緒申鐃緒申鐃緒申鐃緒申鐃祝￥申

鐃熟器申鐃旬ベワ申鐃夙ワ申任鐃緒申襦�

鐃祝は￥申多鐃準式鐃緒申 ${\mathbb{C}}[X]$ 鐃緒申鐃緒申

$% latex2html id marker 834 $\displaystyle X. v= A v \qquad ($$ 鐃緒申鐃縮わ申 $\displaystyle p(X). v =p(A) v)$

(鐃緒申鐃春は刻申鐃緒申肇戰鐃緒申肇鐃塾わ申鐃緒申鐃緒申)鐃夙わ申鐃銃削申鐃術わ申鐃銃わ申鐃暑。鐃宿ッワ申 (.) 鐃緒申鐃緒申鐃春￥申鐃緒申鐃術わ申佑鐃緒申鐃夙わ申鐃祝はわ申鐃縦でもこ鐃塾ドットわ申弔鐃緒申襦�

鐃緒申鐃銃￥申鐃緒申鐃緒申分鐃緒申多鐃準式鐃祝鰹申張鐃緒申鐃銃￥申

$% latex2html id marker 839 $\displaystyle F_0={\mathbb{C}}[X]^n =\left\{ \begi... ..._n(X) \end{pmatrix} ; a_i (X)\in {\mathbb{C}}[X] \quad(i=1,2,\dots,n) \right\} $$

鐃夙わ申鐃緒申鐃塾わ申佑鐃緒申茲�申鐃�

鐃塾醐申 ${}^t(a_1(X),a_2(X),\dots,a_n(X))$ 鐃夙わ申鐃緒申鐃塾わ申鐃緒申鐃緒申的鐃緒申

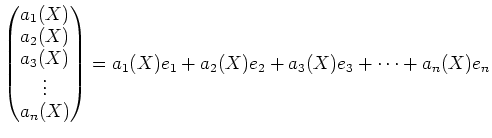
$\displaystyle \begin{pmatrix} a_1(X)\\ a_2(X)\\ a_3(X)\\ \vdots\\ a_n(X) \end{pmatrix} =a_1(X) e_1 +a_2(X) e_2+a_3(X) e_3+ \dots + a_n(X)e_n$

鐃夙書くわ申鐃夙わ申任鐃緒申襦ｏ申鐃緒申辰鐃緒申里曚鐃緒申魯疋奪箸鐃緒申弔鐃緒申覆鐃緒申鐃緒申箸鐃緒申鐃緒申奸鐃� 鐃宿ットや、鐃緒申鐃緒申鐃緒申僂箸龍鐃緒申未鐃縦器申鐃緒申襪随申鐃祝￥申鐃緒申鐃緒申鐃緒申里曚鐃緒申里鐃緒申箸鐃�

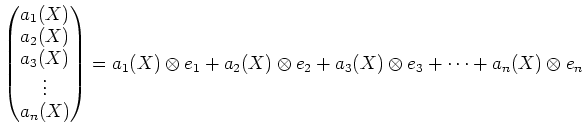
$\displaystyle \begin{pmatrix} a_1(X)\\ a_2(X)\\ a_3(X)\\ \vdots\\ a_n(X) \e... ...(X)\otimes e_1 +a_2(X)\otimes e_2+a_3(X)\otimes e_3+ \dots + a_n(X)\otimes e_n$

鐃夙書くわ申鐃夙もあ鐃暑。( $\otimes$ 鐃熟テンソル記鐃緒申噺討个鐃暑。)

鐃銃ンソル記鐃緒申鐃宿ットわ申鐃瞬わ申鐃緒申鐃緒申鐃緒申鐃緒申鐃緒申 $\phi$ 鐃夙書こわ申鐃緒申鐃緒申鐃淑わ申鐃緒申鐃� $\phi: F_0 \to V$ 鐃緒申

$\displaystyle \phi$	$\displaystyle (a_1(X) \otimes e_1+ a_2(X) \otimes e_2+ a_3(X)\otimes e_3 +\dots+ a_n(X)\otimes e_n)$
$\displaystyle =$	$\displaystyle a_1(X). e_1+ a_2(X) . e_2+ a_3(X). e_3 +\dots+ a_n(X). e_n$
$\displaystyle =$	$\displaystyle a_1(A) e_1+ a_2(A) e_2+ a_3(A) e_3 +\dots+ a_n(A) e_n$

鐃緒申鐃緒申鐃緒申鐃緒申襦�

$\phi$ 鐃緒申鐃緒申鐃緒申鐃緒申鐃緒申鐃叔￥申鐃緒申鐃粛でわ申鐃暑こ鐃夙はわ申鐃緒申鐃緒申分鐃緒申鐃暑。 $\phi$ 鐃塾核は￥申鐃緒申鐃塾よう鐃緒申鐃緒申鐃緒申鐃緒申鐃緒申鐃緒申鐃緒申鐃夙逸申鐃竣わ申鐃暑。

$\displaystyle \psi: F_1={\mathbb{C}}[X]^n \ni L \mapsto (X E -A) L\in {\mathbb{C}}[X]^n=F_0$

$\psi$ 鐃緒申鐃緒申鐃塾器申鐃緒申鐃緒申蟯刻申鐃緒申襪鰹申箸砲鐃獣て￥申鐃叔わ申鐃緒申鐃緒申鐃� 鐃巡さ鐃緒申鐃緒申表鐃緒申鐃祝わ申鐃暑こ鐃夙￥申鐃緒申鐃曙が鐃楯ワ申鐃緒申箸任鐃緒申襦� 鐃渋は￥申鐃塾よう鐃緒申鐃獣種申文鐃緒申妨造蕕削申鐃緒申鐃緒申里茲�申覆笋居申鐃緒申鐃宿緒申鐃緒申鐃緒申鐃緒申襦�

鐃緒申鐃淑わ申鐃緒申鐃� ${\mathbb{C}}[X]$ 鐃叔はユー鐃緒申鐃緒申奪表鐃祝￥申鐃粛常申鐃緒申鐃緒申鐃緒申鐃緒申鐃所算)鐃緒申鐃叔わ申鐃暑こ鐃夙わ申鐃初、鐃緒申鐃楯わ申鐃出わ申法鐃竣わ申鐃夙わ申鐃銃￥申鐃緒申鐃塾よう鐃緒申命鐃所が鐃緒申鐃緒申立鐃縦￥申

命鐃緒申 3.1 $M_n({\mathbb{C}}[X])$ 鐃塾醐申

鐃緒申鐃出わ申鐃銃￥申 ${\mathbb{C}}[X]$ 鐃塾醐申鐃緒申鐃緒申分鐃祝わ申長鐃緒申鐃�

鐃叔￥申 $\operatorname{det}(P)=1,\operatorname{det}(Q)=1$ 鐃緒申鐃緒申鐃緒申鐃緒申鐃緒申

$\displaystyle P B Q= \begin{pmatrix} d_1(X) \\ & d_2 (X) \\ & & d_3(X) \\ & ... ... \\ & & & & & & 0 \\ & & & & & & & \ddots \\ & & & & & & & & 0 \end{pmatrix}$