


: ����ʸ��ˤĤ���...
���������II ���� No.2
�����Υơ���:

���Τ��Ȥ�ͽ���μ��Ȥ����ΤäƤ����ΤȲ��ꤹ�롣
���� 2.1
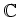
�����Ū���ΤǤ��롣���ʤ����
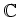
���1�ѿ�¿�༰
(�Ĥޤꡢ
![$ {\mathbb{C}}[X]$](img3.png)
�θ�)�ǡ�����Ǥʤ����
��ɬ�����ʤ��Ȥ��Ĥκ����ġ�
�� 2.1
![$ {\mathbb{C}}[X]$](img3.png)
�θ��ǡ�����Ǥʤ���Τ�ɬ���켡�����Ѥ�ʬ��Ǥ��롣
���ơ�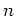 ������������
������������
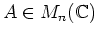 ���Ф��ơ�
���Ф��ơ�
��ɬ���켡��°�Ǥ��뤫�顢
���� 2.1
��˥å���
![$ {\mathbb{C}}[X]\setminus {\mathbb{C}}$](img7.png)
�θ�
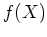
�ǡ�
����������Τ�ɬ��¸�ߤ��롣
�Ȥ������Ȥ�ʬ���롣���Τ褦�� 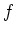 �Τ�����������
�Ǿ��ʤ�Τ�
������������
�Ǿ��ʤ�Τ� 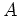 �κǾ�¿�༰�ȸƤ֡��ֵܹ��Ǥϡ�
���Ф餯
�κǾ�¿�༰�ȸƤ֡��ֵܹ��Ǥϡ�
���Ф餯 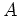 �κǾ�¿�༰�Τ��Ȥ�
�κǾ�¿�༰�Τ��Ȥ� 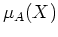 �Ƚ��Ȥˤ��褦��
(
�Ƚ��Ȥˤ��褦��
(
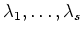 ����ۤʤ�
����ۤʤ� 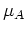 �κ��ǡ�
�κ��ǡ�
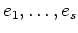 ��
���줾��ν�ʣ��)�Ȱ���ʬ�뤳�Ȥ��Ǥ��롣
��
���줾��ν�ʣ��)�Ȱ���ʬ�뤳�Ȥ��Ǥ��롣
̿�� 2.2
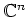
��
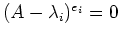
���������褦����ʬ����
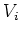
��ľ�¤�
ʬ�뤳�Ȥ��Ǥ��롣���ʤ����
�ʤ뼰��
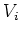
���������ȡ�
��
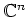
��
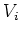
��ľ�¤�ʬ��롣
̿�� 2.3
���Τ褦��
![$ {\mathbb{C}}[X]$](img3.png)
�θ�
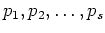
��¸�ߤ��롣
(����Ū��
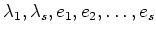
�������ǽ�Ǥ��롣)
-
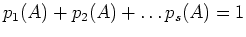
-
-
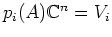
��� 2.1
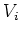
�Τ��Ȥ�
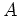
��
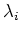
��°������ͭ���֤Ȥ�����
���� 2.1
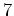
����������
(�Ƥ��ʤ���ʬ������ 0 )���Ф��ơ�̿��
2.3��������
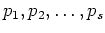
�����Ū��
���衣����ˡ�
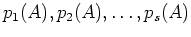
����衣
ʿ��15ǯ10��9��
![]()
![]() ������������
������������
![]() ���Ф��ơ�
���Ф��ơ�