(����)
![]() �ǡ�
�ǡ�![]() ��
�� ![]() �dz���ڤ��Ф褤��
�dz���ڤ��Ф褤��
(����)
�ص���, �ǽ�μ����� ![]() ,���μ�����
,���μ����� ![]() �Ȥ�����
�Ȥ�����
![]() �ʤ�
�ʤ� ![]() �Ȥʤ�Τ��Բ�ǽ�ʤΤǡ�
�Ȥʤ�Τ��Բ�ǽ�ʤΤǡ� ![]() �ξ���ͤ��롣
���ΤȤ���
�ξ���ͤ��롣
���ΤȤ���
![]() �Ǥ��뤫��,
�Ǥ��뤫��,
![]() �ΤȤ���
�ΤȤ���
![]() ��
�� ![]() ���ͤ����פ��뤫�ɤ���Ĵ�٤�Ф褤��
���ͤ����פ��뤫�ɤ���Ĵ�٤�Ф褤��
���ޡ�
![]() �ʤ�����
�ʤ����� ![]() �����ä��Ȥ���ȡ�
�ե���ޤξ������ˤ��
�����ä��Ȥ���ȡ�
�ե���ޤξ������ˤ��
�դ�, ![]() �Ȳ��ꤷ�褦��
�Ȳ��ꤷ�褦��![]() ��
�� ![]() �dz�ä�
����
�dz�ä�
���� ![]() , ���ޤ��
, ���ޤ�� ![]() �Ȥ����ȡ����Ƥ�
�Ȥ����ȡ����Ƥ�
![]() �ˤ�������,
�ˤ�������,
��������˸¤餺�������Ͼ����ʤȤϸ���ʤ��ޤǤ�ʤ��������������������� ����)�����äƤϤ���ư�����Ǥ��롣
(����)
����ϴ�ñ�Ǥ��롣ɸ�� 0 �ʤ�
![]() ��
��
ɸ�������Τ�Τ˴ؤ��Ƥϡ�ɸ�� ![]() ��
��
![]() ��
��
ɸ�� ![]() ��
��
![]() ��,
��,
�ʤɤ�ȿ��ˤ�����Ф褤��
(����)
��������Ϥޤ����äƤ��ä������Τۤ��� ![]() �ˤ��٤��Ǥ��ä���
�ˤ��٤��Ǥ��ä���
![]() �ϴ���Ǥʤ�����Ǥ��롣
�ϴ���Ǥʤ�����Ǥ��롣
����ΤޤޤǤ�, ![]() �ϰ켡�����Ѥ�ʬ��Ǥ��ʤ���
������(�ʤ�ʬ��Ǥ��ʤ����ޤǴޤ)��������Ŧ�ϳ�̵�Ǥ��ä����䤷���¤�Ǥ��롣
�ϰ켡�����Ѥ�ʬ��Ǥ��ʤ���
������(�ʤ�ʬ��Ǥ��ʤ����ޤǴޤ)��������Ŧ�ϳ�̵�Ǥ��ä����䤷���¤�Ǥ��롣
������
![]() �ΰ̿��� 24 �Ǥ��뤳�Ȥ��Ѥ���������ä���
�ΰ̿��� 24 �Ǥ��뤳�Ȥ��Ѥ���������ä���
![]() ��
�� ![]() �ζ�����ʬ��
�ζ�����ʬ��
![]() �������Ǥ��롣
����ʳ��Ϲֵ������������̤�Ǥ��롣
ǰ�Τ���˽Ҥ٤Ƥ����ȡ�
�������Ǥ��롣
����ʳ��Ϲֵ������������̤�Ǥ��롣
ǰ�Τ���˽Ҥ٤Ƥ����ȡ�
![]() �Ȥ�����,
�Ȥ�����,
![]() ���
�������ɬ�פ�����Τ�����
���
�������ɬ�פ�����Τ�����
(1) ![]() ��
��
![]() ��ʿ��������ĤȤ��ˤϡ�
��ʿ��������ĤȤ��ˤϡ�
![]() ����
����
![]() �θ��ο���Ʊ���Ǥ��äơ�
�θ��ο���Ʊ���Ǥ��äơ�![]() �Ǥ��롣
�Ǥ��롣
(2) ![]() ��
��
![]() ��ʿ����������ʤ��Ȥ��ˤ�,
��ʿ����������ʤ��Ȥ��ˤ�,
![]() �����
�θ��Τ��� ![]() �ʳ���
�ʳ���
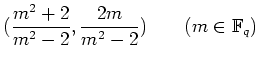
�������ä� ![]() �� modulo
�� modulo ![]() ��ʿ����;�ʤ��,
��ʿ����;�ʤ��,
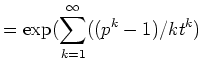 |
||
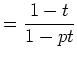 |
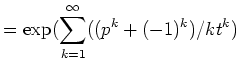 |
||
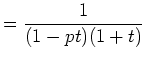 |
���Ȥϡ����̤�,�������� ![]() ���Ф���,
������,
������
![]() ��ʿ����;�ΤȤ�(�Ĥޤ�
��ʿ����;�ΤȤ�(�Ĥޤ� ![]() ��
�� ![]() �dz�ä����ޤ꤬
�dz�ä����ޤ꤬ ![]() �ޤ���
�ޤ��� ![]() �ΤȤ�,
�ΤȤ�,
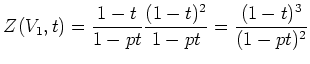
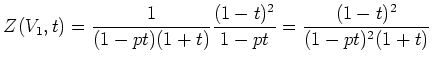
![]() ��ɸ
��ɸ ![]() ���ͤˤ�ä�
���ͤˤ�ä�
![]() �θ���ʬ�ह��Ф褤��
(����ϴ�����Ū�ˤϱ߿���ʿ�̤��ڤ뤳�Ȥˤ�����).
�θ���ʬ�ह��Ф褤��
(����ϴ�����Ū�ˤϱ߿���ʿ�̤��ڤ뤳�Ȥˤ�����).
![]() �ΤȤ��ϡ�
�ΤȤ��ϡ�
![]() �β�ο��������������ᄉ��(
�β�ο��������������ᄉ��(![]() )�ΤϤ��Ǥ��롣
)�ΤϤ��Ǥ��롣
![]() �ΤȤ��ϡ�
�ΤȤ��ϡ�![]() ,
, ![]() ��
�� ![]() ���ѿ��Ѵ����뤳�Ȥˤ��,
���ѿ��Ѵ����뤳�Ȥˤ��,
![]() �롣
���β�ο�������Ʊ��
�롣
���β�ο�������Ʊ�� ![]() �ˤʤ롣���ȤϤ��������Ф褤��
�ˤʤ롣���ȤϤ��������Ф褤��
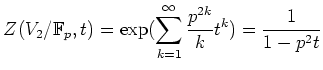
(����)
MuPAD �� powermod �ؿ���Ĥ����д�ñ�Ǥ��ä��������� ![]() �Ǥ��롣
�������äơ��ե���ޤξ��������ж��ˤ��,
�Ǥ��롣
�������äơ��ե���ޤξ��������ж��ˤ��, ![]() ���ǿ��Ǥʤ����Ȥ��狼�롣
ǰ�Τ���ˤ��äƤ�����,
���ǿ��Ǥʤ����Ȥ��狼�롣
ǰ�Τ���ˤ��äƤ�����, ![]() ������ȸ��äơ�
������ȸ��äơ�![]() ��
�ǿ��Ǥ���Ȥϸ¤�ʤ���
��
�ǿ��Ǥ���Ȥϸ¤�ʤ���
powermod �ʤ��Τ�̤Ȥ����ͤΤۤ���¿���Ǥ������� �����������٤�Ȥ��Ф褤��
������ˤ��衢��������Ѥ��ʤ������ݤ�����Ǥ��ä���