


: ����ʸ��ˤĤ���...
�����II ���� No.14

������ա�
¾�ͤ����Ǥˤʤ��Τ�����Ƥϡ����Ǥ�������߲ĤǤ��롣
�������ԥ塼���������ä��ۤ�����ñ�������
��������Τǡ����Τ褦�ʤ�Τ��������Ǥ��ʤ���
(���������ϥ�ݡ�������ǤϤʤ���)
���� 14.1
����
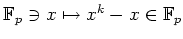
�����ͼ���
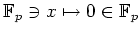
���������������γơ��ξ��������ʤ�����
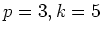 �ΤȤ���
�ΤȤ���
 �ΤȤ���
�ΤȤ���
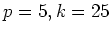 �ΤȤ���
�ΤȤ���
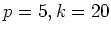 �ΤȤ���
�ΤȤ���
���� 14.2
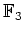
���¿�༰
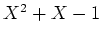
���
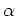
�Ȥ�������
![$ {\mathbb{F}}_{3}[\alpha]$](img11.png)
��¿�༰
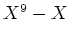
��켡�����Ѥ�ʬ�ʤ�����
���� 14.3
���ǿ�
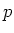
��Ϳ�����Ƥ���Ȥ���Ȥ���
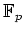
�����������
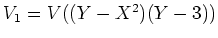
��
��Ʊ�������ؿ�
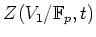
����衣
���� 14.4
���ǿ�
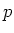
��Ϳ�����Ƥ���Ȥ���Ȥ���
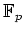
���2�ѿ�����������
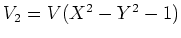
�ι�Ʊ�������ؿ�
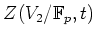
����衣
���� 14.5
���ǿ�
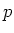
��Ϳ�����Ƥ���Ȥ���Ȥ���
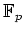
���2�ѿ�����������
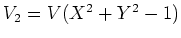
�ι�Ʊ�������ؿ�
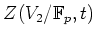
����衣
���� 14.6
���ǿ�
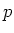
��Ϳ�����Ƥ���Ȥ���Ȥ���
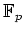
���1�ѿ�����������
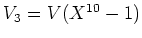
�ι�Ʊ�������ؿ�
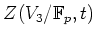
����衣
2002ǯ8��15��
![]()