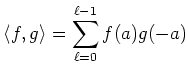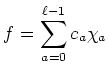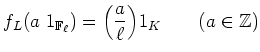: ïŋ―ïŋ―ïŋ―ïŋ―Ęļïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―...
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―II ïŋ―ïŋ―ïŋ―ïŋ― No.13
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĨÆĄïŋ―ïŋ―ïŋ―:

ïŋ―ïŋ―ïŋ―ïŋ―Ęŋïŋ―ïŋ―ïŋ―ïŋ―Íūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―˥§ïŋ―Îūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪÃĪÆĪïŋ―ïŋ―ÞĪÃĪÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÂĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĪÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ― 13.1
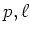
ïŋ―ïŋ―ïŋ―ïŋ―ÛĪĘĪïŋ―ïŋ―ïŋ―Įŋïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
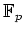
ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―
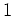
ïŋ―Îļïŋ―ïŋ―ïŋ―
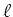
-ïŋ―蚎
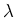
ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―
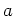
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―Íïŋ―ïŋ―ïŋ―ÎĪÎĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
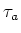
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
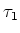
ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ―Ãąïŋ―ïŋ―
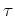
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÄĪïŋ―ïŋ―ĮĪËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ΰïŋ―ĖĢïŋ―ËĪÄĪïŋ―ïŋ―ÆĪâĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŌĪŲĪÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 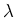 ïŋ―Ïžïŋ―ïŋ―ÎĪčĪĶïŋ―ËĪïŋ―ïŋ―ÆĪČĪëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―Ïžïŋ―ïŋ―ÎĪčĪĶïŋ―ËĪïŋ―ïŋ―ÆĪČĪëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
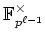 ïŋ―Ï°Ėŋïŋ―
ïŋ―Ï°Ėŋïŋ―
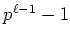 ïŋ―Î―ïŋ―ó·ēĪĮĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Î―ïŋ―ó·ēĪĮĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 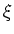 ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÕĨïŋ―ïŋ―ïŋ―ÞĄïŋ―ïŋ―Îūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÕĨïŋ―ïŋ―ïŋ―ÞĄïŋ―ïŋ―Îūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―
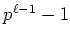 ïŋ―ïŋ―
ïŋ―ïŋ― 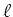 ïŋ―Įģïŋ―ïŋ―ïŋ―ÚĪïŋ―ëĪŦïŋ―éĄĒ
ïŋ―Įģïŋ―ïŋ―ïŋ―ÚĪïŋ―ëĪŦïŋ―éĄĒ
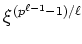 ïŋ―ïŋ―ÍĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―Îļïŋ―ïŋ―ïŋ―
ïŋ―Ėŋïŋ―ïŋ―ÏĪïŋ―ïŋ―įĪĶïŋ―ïŋ―
ïŋ―ïŋ―ÍĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―Îļïŋ―ïŋ―ïŋ―
ïŋ―Ėŋïŋ―ïŋ―ÏĪïŋ―ïŋ―įĪĶïŋ―ïŋ― 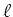 ïŋ―ĮĪïŋ―ïŋ―ëĪŦïŋ―éĄĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĪŦïŋ―éĄĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 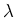 ïŋ―ČĪïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĘĪïŋ―ïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĘĪïŋ―ïŋ―ïŋ―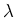 ïŋ―Ξïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ï°ïŋ―ïŋ―ÅŠïŋ―ĮĪÏĪĘĪïŋ―ïŋ―ïŋ―
1ïŋ―ïŋ―
ïŋ―Ξïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ï°ïŋ―ïŋ―ÅŠïŋ―ĮĪÏĪĘĪïŋ―ïŋ―ïŋ―
1ïŋ―ïŋ― 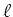 ïŋ―蚎ïŋ―ïŋ―
ïŋ―蚎ïŋ―ïŋ― 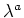
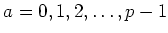 ïŋ―ïŋ―
ïŋ―ïŋ― 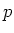 ïŋ―ÄĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÄĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 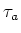 ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(1)ïŋ―ÏĪïŋ―ïŋ―ïŋ―éĪŽïŋ―ïŋ―ïŋ―Κïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ŌĪŲĪÆĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(1)ïŋ―ÏĪïŋ―ïŋ―ïŋ―éĪŽïŋ―ïŋ―ïŋ―Κïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ŌĪŲĪÆĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―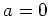 ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĖĪĮĄïŋ―
ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĖĪĮĄïŋ―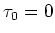 ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĄïŋ―
ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 13.1 (Ęŋïŋ―ïŋ―ïŋ―ïŋ―Íūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―˥§)
ïŋ―ïŋ―ïŋ―Įŋïŋ―
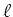
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―Æžïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĄïŋ―
-
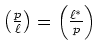 (ÃĒïŋ―ïŋ―
(ÃĒïŋ―ïŋ―
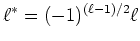 )
)
ïŋ―ïŋ―ïŋ―ïŋ― 13.1
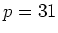
,
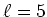
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
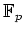
ïŋ―ïŋ―
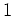
ïŋ―Îļïŋ―ïŋ―ïŋ―
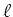
-ïŋ―蚎ïŋ―ïŋ―
ïŋ―ïŋ―Äļïŋ―ïŋ―ÄĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
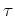
ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
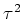
ïŋ―ïŋ―šÝĪË·Ũŧïŋ―ïŋ―ïŋ―ïŋ―ÆĪßĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 13.2
ïŋ―ïŋ―ïŋ―Įŋïŋ―
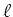
ïŋ―ČĄïŋ―ïŋ―ïŋ―
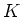
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ÆĄïŋ―
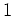
ïŋ―Îļïŋ―ïŋ―ïŋ―
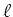
ïŋ―蚎
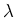
ïŋ―ïŋ―
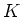
ïŋ―ÎĪĘĪïŋ―ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
(ïŋ―ČĪïŋ―ïŋ―ËĄïŋ―
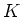
ïŋ―ïŋ―Éļïŋ―ïŋ―ïŋ―ïŋ―
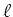
ïŋ―ĮĪÏĪĘĪïŋ―ïŋ―ïŋ―)
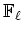
ïŋ―ïŋ―ïŋ―
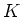
-ïŋ―ÍīØŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
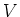
ïŋ―ïŋ― (ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪÎēïŋ―ËĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―饞ïŋ―ÜĪËĪïŋ―ïŋ―)
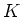
ïŋ―ïŋ―ÎĨŲĨïŋ―ïŋ―ČĨïŋ―ïŋ―ïŋ―ÖĪËĪĘĪęĄĒ
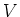
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÞĪëĄĢ(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)
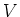 ïŋ―ïŋ―
ïŋ―ïŋ― 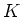 ïŋ―ïŋ―Ξïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ(ïŋ―ïŋ―ïŋ―ÎĪßĪĮĪčĪĪïŋ―ïŋ―)
ïŋ―ïŋ―Ξïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ(ïŋ―ïŋ―ïŋ―ÎĪßĪĮĪčĪĪïŋ―ïŋ―)
- (ïŋ―ïŋ―Éļïŋ―ïŋ―Äūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)
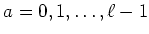 ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―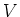 ïŋ―Îļïŋ―
ïŋ―Îļïŋ― 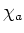 ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
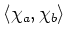 ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
-
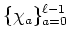 ïŋ―ïŋ―
ïŋ―ïŋ― 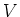 ïŋ―Îīïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―
ïŋ―Îīïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―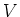 ïŋ―Îļïŋ―
ïŋ―Îļïŋ― 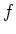 ïŋ―ïŋ―
ïŋ―Č―ņĪŊĪïŋ―ïŋ―ïŋ―ËĪÏĄïŋ―
ïŋ―ïŋ―
ïŋ―Č―ņĪŊĪïŋ―ïŋ―ïŋ―ËĪÏĄïŋ― 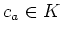 ïŋ―ïŋ―ÉĪÎĪčĪĶïŋ―Ëĩïŋ―ïŋ―ïŋ―ÐĪčĪĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŌĪŲĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ÉĪÎĪčĪĶïŋ―Ëĩïŋ―ïŋ―ïŋ―ÐĪčĪĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŌĪŲĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 13.3
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îēïŋ―ïŋ―ĮĄïŋ―
ïŋ―ÕĄïŋ―ïŋ―ęĨĻïŋ―Ņīïŋ―
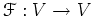
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
-
![$ \langle \mathcal F[f],\chi_a\rangle =\ell f(-a)$](img46.png) ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĪïŋ―ïŋ―ïŋ―
ïŋ―ōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĪïŋ―ïŋ―ïŋ―
ïŋ―ōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
-
![$ \mathcal F[\mathcal F[f]]$](img47.png) ïŋ―ïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
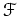 ïŋ―Îĩïŋ―ïŋ―Ņīïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Îĩïŋ―ïŋ―Ņīïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
- ĮĪïŋ―ÕĪïŋ―
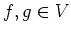 ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
![$ \langle \mathcal F[f],g \rangle=\langle f,\mathcal F [g]\rangle$](img50.png) ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĪïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĪïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
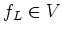 ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ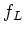 ïŋ―ïŋ―
ïŋ―ïŋ―
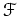 ïŋ―Îļïŋ―Íïŋ―ŲĨïŋ―ïŋ―ČĨïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ėĪŽÂ°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Íïŋ―ÍĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Îļïŋ―Íïŋ―ŲĨïŋ―ïŋ―ČĨïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪōžĻĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ėĪŽÂ°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Íïŋ―ÍĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
2002ĮŊ7ïŋ―ïŋ―15ïŋ―ïŋ―
![]()
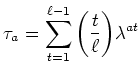
![]() ïŋ―Ïžïŋ―ïŋ―ÎĪčĪĶïŋ―ËĪïŋ―ïŋ―ÆĪČĪëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―Ïžïŋ―ïŋ―ÎĪčĪĶïŋ―ËĪïŋ―ïŋ―ÆĪČĪëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
![]() ïŋ―Ï°Ėŋïŋ―
ïŋ―Ï°Ėŋïŋ―
![]() ïŋ―Î―ïŋ―ó·ēĪĮĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Î―ïŋ―ó·ēĪĮĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÕĨïŋ―ïŋ―ïŋ―ÞĄïŋ―ïŋ―Îūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÕĨïŋ―ïŋ―ïŋ―ÞĄïŋ―ïŋ―Îūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―
![]() ïŋ―ïŋ―
ïŋ―ïŋ― ![]() ïŋ―Įģïŋ―ïŋ―ïŋ―ÚĪïŋ―ëĪŦïŋ―éĄĒ
ïŋ―Įģïŋ―ïŋ―ïŋ―ÚĪïŋ―ëĪŦïŋ―éĄĒ
![]() ïŋ―ïŋ―ÍĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―Îļïŋ―ïŋ―ïŋ―
ïŋ―Ėŋïŋ―ïŋ―ÏĪïŋ―ïŋ―įĪĶïŋ―ïŋ―
ïŋ―ïŋ―ÍĪïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―Îļïŋ―ïŋ―ïŋ―
ïŋ―Ėŋïŋ―ïŋ―ÏĪïŋ―ïŋ―įĪĶïŋ―ïŋ― ![]() ïŋ―ĮĪïŋ―ïŋ―ëĪŦïŋ―éĄĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĪŦïŋ―éĄĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ČĪïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĘĪïŋ―ïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĘĪïŋ―ïŋ―ïŋ―![]() ïŋ―Ξïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ï°ïŋ―ïŋ―ÅŠïŋ―ĮĪÏĪĘĪïŋ―ïŋ―ïŋ―
1ïŋ―ïŋ―
ïŋ―Ξïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ï°ïŋ―ïŋ―ÅŠïŋ―ĮĪÏĪĘĪïŋ―ïŋ―ïŋ―
1ïŋ―ïŋ― ![]() ïŋ―蚎ïŋ―ïŋ―
ïŋ―蚎ïŋ―ïŋ― ![]()
![]() ïŋ―ïŋ―
ïŋ―ïŋ― ![]() ïŋ―ÄĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÄĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(1)ïŋ―ÏĪïŋ―ïŋ―ïŋ―éĪŽïŋ―ïŋ―ïŋ―Κïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ŌĪŲĪÆĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(1)ïŋ―ÏĪïŋ―ïŋ―ïŋ―éĪŽïŋ―ïŋ―ïŋ―Κïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ŌĪŲĪÆĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―![]() ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĖĪĮĄïŋ―
ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĖĪĮĄïŋ―![]() ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĄïŋ―
ïŋ―ïŋ―ïŋ―ĘĪęĪŋïŋ―ÄĄïŋ―
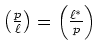 (ÃĒïŋ―ïŋ―
(ÃĒïŋ―ïŋ―