ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĨÆĄïŋ―ïŋ―ïŋ―:
![]()
ïŋ―ïŋ―ïŋ―óĄĒžïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ęĪŽïŋ―ÄĪÃĪÆĪïŋ―ïŋ―ÞĪÃĪÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĖĪËĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Øŋïŋ―ïŋ―ïŋ― ![]() ïŋ―ËĪïŋ―ÃĪÆĪÉĪÎĪčĪĶïŋ―ïŋ―ïŋ―ŅĪïŋ―ëĪŦïŋ―ïŋ―ĘĢïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ãĪĻïŋ―ïŋ―
ïŋ―ËĪïŋ―ÃĪÆĪÉĪÎĪčĪĶïŋ―ïŋ―ïŋ―ŅĪïŋ―ëĪŦïŋ―ïŋ―ĘĢïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ãĪĻïŋ―ïŋ― ![]() ïŋ―Ïģïŋ―ïŋ―Įŋïŋ―
ïŋ―Ïģïŋ―ïŋ―Įŋïŋ― ![]() ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―
![]() ïŋ―ïŋ―ïŋ―Âŋïŋ―āž°ïŋ―Čļïŋ―ïŋ―ïŋ―ïŋ―ëĪŽïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ėĪŽïŋ―ïŋ―ïŋ―óĪŦĪÉĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―Âŋïŋ―āž°ïŋ―Čļïŋ―ïŋ―ïŋ―ïŋ―ëĪŽïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ėĪŽïŋ―ïŋ―ïŋ―óĪŦĪÉĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ËĪïŋ―ÃĪÆ°ÛĪĘĪëĄĢ
ïŋ―ÉĪÎĪčĪĶïŋ―ïŋ―
ïŋ―ËĪïŋ―ÃĪÆ°ÛĪĘĪëĄĢ
ïŋ―ÉĪÎĪčĪĶïŋ―ïŋ― ![]() ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―Æīïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪŦïŋ―ïŋ―Č―ïŋ―ęĪđïŋ―ïŋ―ÎĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪÎĪïŋ―ïŋ―ïŋ―Ęŋïŋ―ïŋ―ïŋ―ïŋ―Íūïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―˥§ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―˥§ïŋ―Îūïŋ―ïŋ―ïŋ―ïŋ―ÏĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĪŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎđÖĩïŋ―ïŋ―ïŋ―ïŋ―ÃĪÎąïŋ―ïŋ―ŅĪČĪïŋ―ïŋ―ïŋ―
Íïŋ―ïŋ―ïŋ―Îūïŋ―ÎĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÂĪïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŌēðĪđĪëĄĢ
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―Æīïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪŦïŋ―ïŋ―Č―ïŋ―ęĪđïŋ―ïŋ―ÎĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪÎĪïŋ―ïŋ―ïŋ―Ęŋïŋ―ïŋ―ïŋ―ïŋ―Íūïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―˥§ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―˥§ïŋ―Îūïŋ―ïŋ―ïŋ―ïŋ―ÏĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ëĪŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎđÖĩïŋ―ïŋ―ïŋ―ïŋ―ÃĪÎąïŋ―ïŋ―ŅĪČĪïŋ―ïŋ―ïŋ―
Íïŋ―ïŋ―ïŋ―Îūïŋ―ÎĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÂĪïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŌēðĪđĪëĄĢ
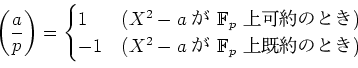
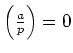 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
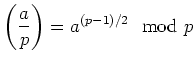
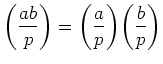
ïŋ―ČĪïŋ―ïŋ―ïŋ―
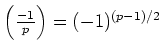 ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÕĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÕĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
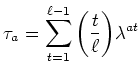
(ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―Ę·Ũŧïŋ―ïŋ―ōĪ·Īïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ÎĪïŋ―ïŋ―ïŋ― ïŋ―ïŋ―ïŋ―ΰïŋ―ÄĪÎĨŌĨïŋ―ČĪÏĨÕĄïŋ―ïŋ―ęĨĻïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ëĄĢ)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―Čžïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢÃĒïŋ―ïŋ―(3)ïŋ―Îūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ëūïŋ―ïŋ―ëĄĢ
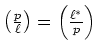 (ÃĒïŋ―ïŋ―
(ÃĒïŋ―ïŋ―
![]() ïŋ―Κïŋ―ïŋ―ïŋ―
ïŋ―Κïŋ―ïŋ―ïŋ― ![]() ïŋ―ČĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
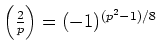 ïŋ―ōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―